In this article, we will explore the problem of finding the intersections of two lists of closed intervals. We will walk through the problem definition, understand the brute force approach (if applicable), and then dive into a more efficient approach to solve the problem. Finally, we’ll provide a challenge for readers who want to further their understanding and a conclusion to summarize our findings.

If you’re just joining us, it might be helpful to catch up on the previous entries. Want to see more problem-solving techniques? Follow me here on my blog!


Understanding the Problem#
Given two lists of closed intervals, firstList and secondList, we need to determine the intersection of these two interval lists. Each interval is represented as [start, end], and the intersection of two closed intervals is the set of real numbers that belong to both intervals. If the intersection is not empty, it is also represented as a closed interval.
Example 1:
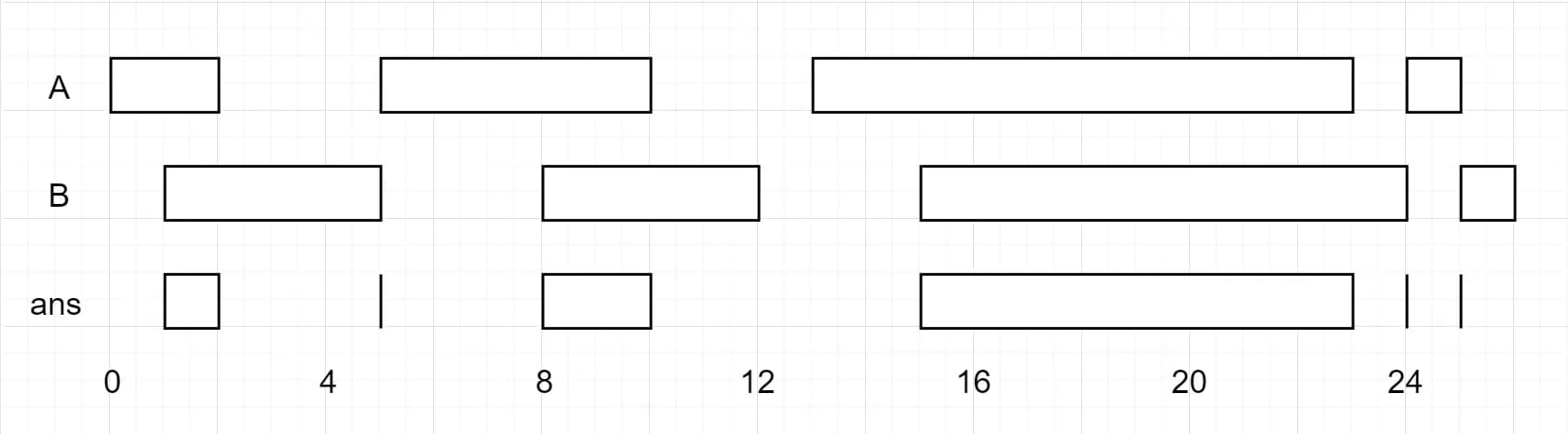
Input: firstList = [[0,2],[5,10],[13,23],[24,25]], secondList = [[1,5],[8,12],[15,24],[25,26]]
Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]
Example 2:
Input: firstList = [[1,3],[5,9]], secondList = []
Output: []
Using Efficient Approach (Two-Pointer Technique)#
To solve this problem efficiently, we can leverage the fact that both interval lists are pairwise disjoint and sorted. By using a two-pointer technique, we can find intersections without comparing each interval with every other interval.
The two-pointer technique involves using two pointers to iterate through both interval lists simultaneously. We compare the current intervals from both lists to determine if there is an intersection. If there is, we add it to our result. Depending on which interval ends first, we move the corresponding pointer forward.
def intervalIntersection(
self, firstList: List[List[int]], secondList: List[List[int]]
) -> List[List[int]]:
ans = []
i, j = 0, 0
while i < len(firstList) and j < len(secondList):
lo = max(firstList[i][0], secondList[j][0])
hi = min(firstList[i][1], secondList[j][1])
if lo <= hi:
ans.append([lo, hi])
if firstList[i][1] < secondList[j][1]:
i += 1
else:
j += 1
return ans
Explanation#
- Initialization: We initialize an empty list
ansto store the result and two pointersiandjto iterate throughfirstListandsecondList, respectively. - Loop through lists: We use a
whileloop to iterate as long as both pointers are within the bounds of their respective lists. - Find intersection: For the current intervals
firstList[i]andsecondList[j], we calculate the intersection boundsloandhi.lois the maximum of the start points, andhiis the minimum of the end points. - Check for valid intersection: If
lois less than or equal tohi, there is an intersection, and we append[lo, hi]toans. - Move pointers: We increment the pointer of the interval that ends first. If
firstList[i][1]is less thansecondList[j][1], we incrementi. Otherwise, we incrementj. - Return result: After the loop,
anscontains all the intersections.
Time Complexity: O(n + m), where n is the length of firstList and m is the length of secondList. We iterate through both lists once.
Space Complexity: O(1) for extra space, excluding the space required for the output list ans.
Conclusion#
In this article, we tackled the problem of finding the intersections of two lists of closed intervals. We discussed an efficient two-pointer approach to solve the problem and analyzed its time and space complexity. By leveraging the sorted nature of the input lists, we were able to find the solution efficiently.
Understanding these methods enhances your problem-solving skills and prepares you for tackling similar challenges in coding interviews and competitions.
Found this helpful? Follow me for more leetcode adventures! Questions? React out via email.
