A LeetCode Daily Series — Day 88

In this article, we’ll explore the problem of rotating a linked list to the right by a given number of places. We’ll delve into the problem, discuss an efficient solution, and provide detailed explanations for better understanding. Let’s get started!

Rotate List - LeetCode leetcode.com

Can you solve this real interview question? Rotate List

If you’re just joining us, it might be helpful to catch up on the previous entries. Want to see more problem-solving techniques? Follow me here on my blog!

A LeetCode Daily Series — Introduction | Ritesh Shakya riteshakya.com.np

Hey everyone, I’m excited to announce that I’m embarking on a journey to conquer LeetCode!

Cover Image

Understanding the Problem

Given the head of a linked list, the task is to rotate the list to the right by k places. Here’s an example to illustrate:

Example 1:

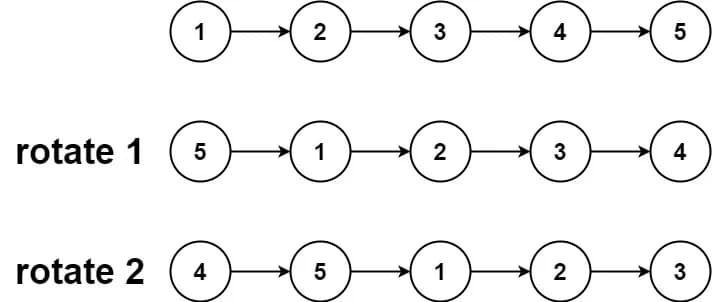
Input: head = [1,2,3,4,5], k = 2
Output: [4,5,1,2,3]

Example 2:

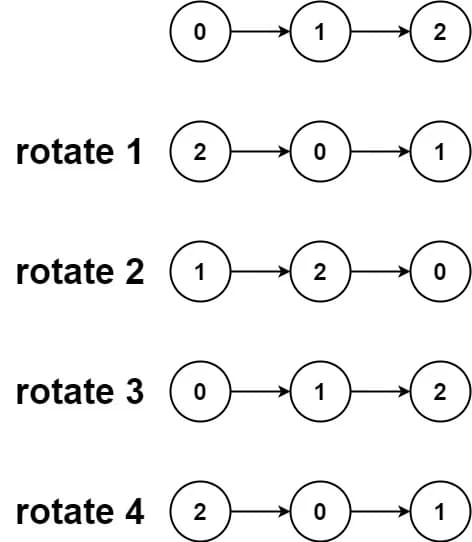
Input: head = [0,1,2], k = 4
Output: [2,0,1]

Using Efficient Approach: Circular Linked List Conversion

The main idea behind this approach is to first convert the given linked list into a circular linked list. By connecting the last node to the head, we create a loop that allows us to easily determine the new head after rotating the list. Here’s the step-by-step breakdown:

Calculate the Length: Traverse the list to determine its length.
Form a Circular List: Connect the last node to the head, forming a circular list.
Determine Effective Rotations: Since rotating the list by its length results in the same list, we use k % length to get the effective number of rotations.
Find the New Head: Traverse the list to find the new head after the rotations.
Break the Circle: Disconnect the circular link to return to a regular linked list.

def rotateRight(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:
    if not head or not head.next:
        return head

    # Calculate the length of the list
    length = 1
    last_ele = head
    while last_ele.next is not None:
        last_ele = last_ele.next
        length += 1

    # Form a circular linked list
    last_ele.next = head

    # Effective rotations
    k = k % length

    # Find the new head after rotating
    curr = head
    for x in range(length - k - 1):
        curr = curr.next

    # Break the circular list to form the result
    answer = curr.next
    curr.next = None
    return answer

Explanation

Base Cases: If the list is empty or contains only one node, return the head as is.
Calculate Length: Traverse the list to calculate its length. During this traversal, keep track of the last element.
Form a Circular List: Connect the last node’s next to the head, forming a circular linked list.
Effective Rotations: Calculate the effective number of rotations using k % length.
Find the New Head: Traverse the list to find the new head position after the rotations.
Break the Circle: Disconnect the circular link to return to a regular linked list, and return the new head.

Time Complexity: O(N), where N is the number of nodes in the linked list. We traverse the list a couple of times: once to calculate the length and once to find the new head.

Space Complexity: O(1), as we are using a constant amount of extra space.

Result