A LeetCode Daily Series — Day 86

Today’s problem is called "Number of Islands"

Updated: at 02:25 AM

In this article, we delve into the problem of counting the number of islands in a 2D binary grid. This is a common problem in coding interviews and competitive programming. We will explore the problem, understand the brute force approach, and then move on to more efficient solutions.

If you’re just joining us, it might be helpful to catch up on the previous entries. Want to see more problem-solving techniques? Follow me here on my blog!

Cover Image

Understanding the Problem

Given an m x n 2D binary grid where ‘1’ represents land and ‘0’ represents water, the task is to count the number of islands. An island is defined as a group of adjacent lands connected horizontally or vertically. All four edges of the grid are surrounded by water.

Example 1:

Input: grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
Output: 1

Example 2:

Input: grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
Output: 3

To solve this problem efficiently, we can use the Breadth-First Search (BFS) algorithm. The idea is to iterate over each cell in the grid. If we encounter a ‘1’, it means we’ve found an island. We then use BFS to traverse all connected lands and mark them as visited.

def numIslands(self, grid: List[List[str]]) -> int:
    if not grid:
        return 0

    rows, cols = len(grid), len(grid[0])
    islands = 0

    def bfs(r, c):
        q = collections.deque()
        visit.add((r, c))
        q.append((r, c))

        while q:
            row, col = q.popleft()
            directions = [[1, 0], [-1, 0], [0, 1], [0, -1]]

            for dr, dc in directions:
                r, c = row + dr, col + dc
                if (
                    r in range(rows)
                    and c in range(cols)
                    and grid[r][c] == "1"
                    and (r, c) not in visit
                ):
                    grid[r][c] == "0"
                    q.append((r, c))

    for r in range(rows):
        for c in range(cols):
            if grid[r][c] == "1":
                bfs(r, c)
                islands += 1

    return islands

Explanation

  1. Initialization:
    • rows and cols store the dimensions of the grid.
    • visit is a set to keep track of the cells that have been visited.
    • islands is a counter to keep track of the number of islands.
  2. BFS Function:
    • The bfs function is called when we find a '1' in the grid.
    • A deque q is used to facilitate the breadth-first search.
    • The starting cell (r, c) is added to the visit set and the deque.
    • While the deque is not empty, we process each cell by checking its neighbors in four possible directions: down, up, right, and left.
    • If a neighboring cell is within bounds, contains a '1', and has not been visited, it is added to the deque and marked as visited.
  3. Main Loop:
    • We iterate through each cell in the grid using nested loops.
    • If we find a '1' that has not been visited, it signifies the start of a new island.
    • We call the bfs function to mark all cells connected to this '1' as visited.
    • We increment the islands counter for each new island found.

Time Complexity: O(m x n), where m is the number of rows and n is the number of columns. Each cell is visited once.

Space Complexity: O(min(m, n)) for the BFS queue, as the queue can at most contain the cells of the smallest dimension of the grid.

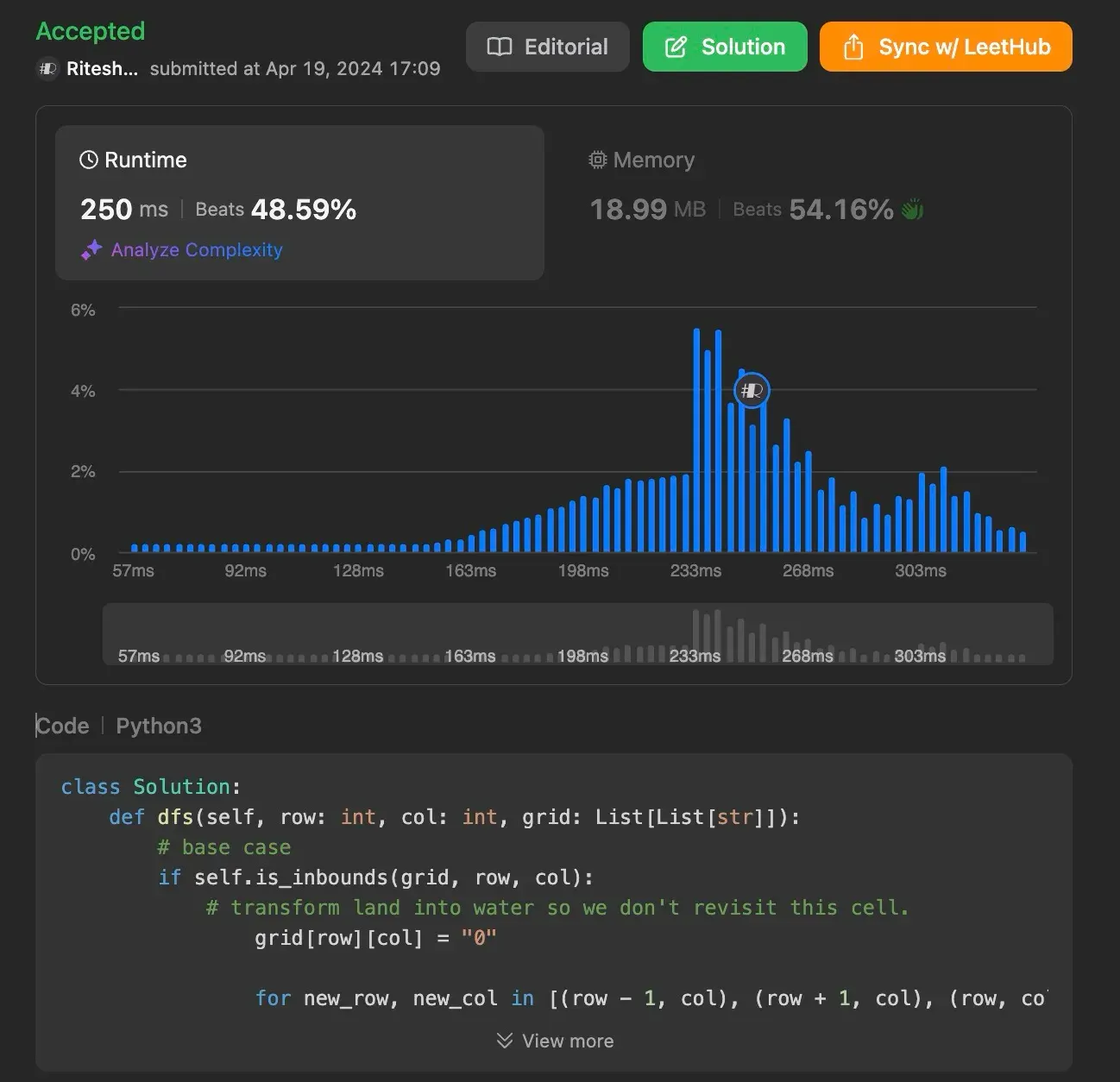
BFS Result

Another efficient way to solve this problem is using the Depth-First Search (DFS) algorithm. Similar to BFS, we iterate over the grid, and when we find a ‘1’, we use DFS to mark all connected lands.

class Solution:
    def numIslands(self, grid: List[List[str]]) -> int:
        if not grid:
            return 0
        rows = len(grid)
        cols = len(grid[0])
        islands = 0

        def dfs(r, c):
            if r not in range(rows) or c not in range(cols) or grid[r][c] == "0":
                return
            grid[r][c] = "0"
            dfs(r + 1, c)
            dfs(r - 1, c)
            dfs(r, c + 1)
            dfs(r, c - 1)

        for r in range(rows):
            for c in range(cols):
                if grid[r][c] == "1":
                    islands += 1
                    dfs(r, c)
        return islands

Explanation

  1. Initialization:
    • rows and cols store the number of rows and columns in the grid, respectively.
    • islands is initialized to 0 to keep track of the number of islands.
  2. DFS Function:
    • The dfs function is defined to recursively mark the connected lands.
    • It takes coordinates (r, c) as input and checks if the cell is out of bounds or contains 0. If so, it returns immediately.
    • If the cell contains 1, it is part of an island and is marked as 0 (visited).
    • The function then recursively calls itself for the neighboring cells: down, up, right, and left.
  3. Main Loop:
    • We iterate over each cell in the grid using nested loops.
    • When we find a 1, it indicates the start of a new island.
    • We call the dfs function to mark all cells connected to this 1 as visited.
    • We increment the islands for each new island found.

Time Complexity: O(m x n), where m is the number of rows and n is the number of columns. Each cell is visited once.

Space Complexity: O(1) as this modies the existing grid without adding any extra space besides, rows, cols and count.

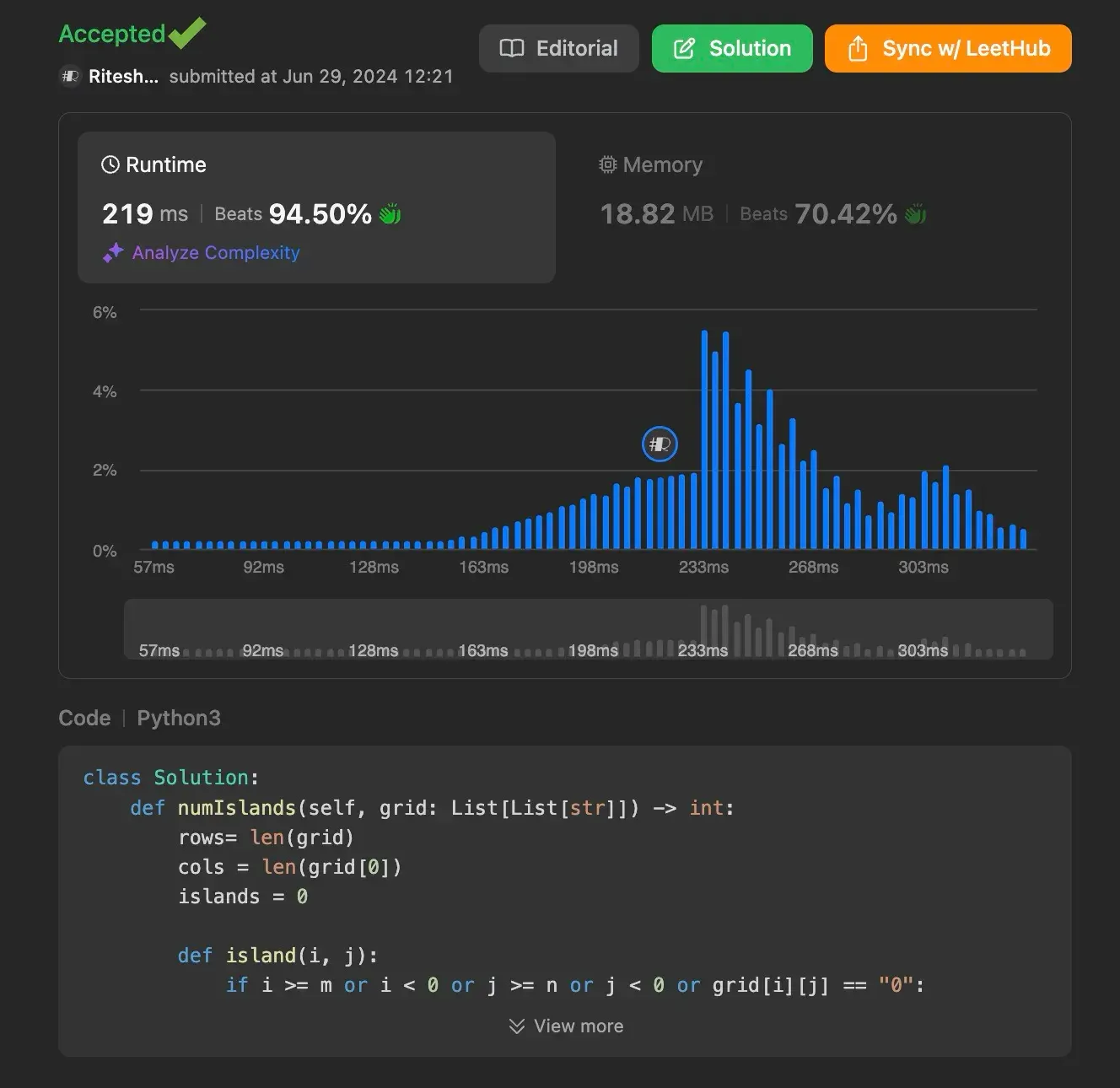
DFS Result

Conclusion

Counting the number of islands in a 2D grid is an interesting problem that can be efficiently solved using graph traversal algorithms like BFS and DFS. Both methods ensure that we visit each cell once, providing optimal solutions.

Understanding these methods enhances your problem-solving skills and prepares you for tackling similar challenges in coding interviews and competitions.

Found this helpful? Follow me for more leetcode adventures! Questions? React out via email.

Next Articles in the Series