A LeetCode Daily Series — Day 84

In this article, we delve into the problem of reordering a singly linked list and explore two approaches to solve it efficiently. The task involves rearranging the nodes of the list to achieve a specific order. Let’s begin by understanding the problem.

Reorder List - LeetCode leetcode.com

Can you solve this real interview question? Reorder List

If you’re just joining us, it might be helpful to catch up on the previous entries. Want to see more problem-solving techniques? Follow me here on my blog!

A LeetCode Daily Series — Introduction | Ritesh Shakya riteshakya.com.np

Hey everyone, I’m excited to announce that I’m embarking on a journey to conquer LeetCode!

Understanding the Problem

Given the head of a singly linked list, we are to reorder the list in a specific manner:

L0 → Ln → L1 → Ln-1 → L2 → Ln-2 → ...

We may not modify the values in the list’s nodes but can change the nodes themselves.

Example 1:

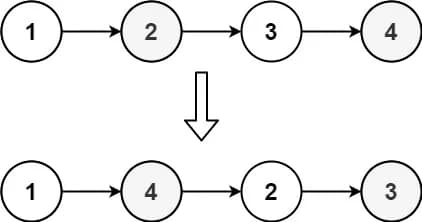
Input: head = [1,2,3,4]
Output: [1,4,2,3]

Example 2:

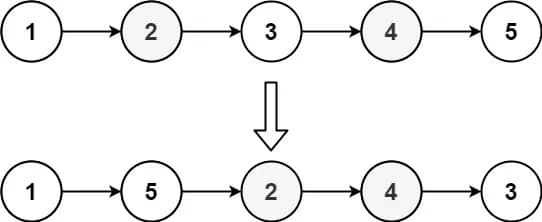
Input: head = [1,2,3,4,5]
Output: [1,5,2,4,3]

Using Efficient Approach 1: Deque-Based Approach

The first approach uses a deque to reorder the list. This method involves storing nodes in a deque and then rearranging them by alternating between the front and back of the deque.

def reorderList(self, head: Optional[ListNode]) -> None:

    queue = collections.deque()
    currentNode = head.next

    while currentNode:
        queue.append(currentNode)
        currentNode = currentNode.next

    currentNode = head
    while len(queue) > 1:
        currentNode.next = queue.pop()
        currentNode = currentNode.next
        currentNode.next = queue.popleft()
        currentNode = currentNode.next

    if queue:
        currentNode.next = queue.pop()
        currentNode = currentNode.next

    currentNode.next = None

Explanation

1. Initialization:
   • A deque is initialized to store the nodes of the linked list except for the head node.
   • currentNode is initialized to the node next to the head.
2. Populating the Deque:
   • Traverse the linked list and add each node (except the head) to the deque.
3. Reordering the List:
   • Iterate through the linked list, linking nodes alternatively from the front and back of the deque.
   • Connect the currentNode to the last node from the deque, then to the first node from the deque.
   • If there are remaining nodes in the deque, connect the currentNode to the last remaining node.
4. Final Adjustment:
   • Ensure the last node points to None to avoid cycles.

How it works

What is happening above? Think about how deque works., for the following testcase:

Test case: [1, 2, 3, 4, 5]
Output AC: [1, 5, 2, 4, 3]

So, If we append every node into deque. Our deque will be : [ 2, 3, 4, 5 ]

  deque = [2, 3, 4, 5]
           ^        ^
           |        |
    popleft()        pop()
    O(1)T            O(1)T

If we pop() then popleft() on each iteration it get popped like this : 5, 2, 4, 3 . So all we need to do is, based on the popped elements, update the head.next.

Time Complexity: O(n), because we traverse the list once to populate the deque and once more to reorder it.

Space Complexity: O(n), because we store all nodes in the deque.

Using Efficient Approach 2: Two-Pointer Technique

The second approach uses the two-pointer technique to achieve the desired reordering. This involves finding the middle of the list, reversing the second half, and merging the two halves in the required order.

def reorderList(self, head: Optional[ListNode]) -> None:\
    leftHead = head
    slow = head
    fast = head.next

    while fast and fast.next:
        slow = slow.next
        fast = fast.next.next

    rightHead = slow.next
    slow.next = None

    prev, curr = None, rightHead
    while curr:
        temp = curr.next
        curr.next = prev
        prev = curr
        curr = temp

    rightHead = prev

    while rightHead:
        leftTemp, rightTemp = leftHead.next, rightHead.next

        leftHead.next = rightHead
        rightHead.next = leftTemp

        leftHead = leftTemp
        rightHead = rightTemp

Explanation

1. Finding the Middle of the List:
   • Use slow and fast pointers to find the middle. Slow moves one step at a time, while fast moves two steps at a time.
2. Cutting the List into Two Halves:
   • Split the list into two halves. The left half remains connected, and the right half starts from the node after the middle node.
   • This is achieved in the code by setting the rightHead pointer to the node after the middle node (slow.next) and then disconnecting the left half from the right half by setting slow.next to None.
3. Reversing the Second Half:
   • Reverse the second half of the list by using the prev, curr, and temp pointers to reverse the next pointers in each node of the right half.
4. Merging the Two Halves:

   # This is how our list looks at this point
   """
   [ 1 -> 2 -> 3 ]    [4 <- 5 <- 6]
       ^                           ^
       |                           |
       leftHead            rightHead
   """
   

   • Merge the two halves by alternating nodes from each half by iterating through the left and right halves simultaneously and updating the next pointers of the nodes to achieve the desired order.

Time Complexity: O(n), because we traverse the list to find the middle, reverse the second half, and then merge the halves.

Space Complexity: O(1), because we only use a constant amount of extra space.

Conclusion

Reordering a linked list can be efficiently achieved using either a deque-based approach or a two-pointer technique. While the deque method is straightforward, the two-pointer technique offers an optimal solution in terms of space complexity.

Understanding these methods enhances your problem-solving skills and prepares you for tackling similar challenges in coding interviews and competitions.

Found this helpful? Follow me for more leetcode adventures! Questions? React out via email.

Next Articles in the Series

A LeetCode Daily Series — Day 85 | Ritesh Shakya riteshakya.com.np

Today’s problem is called "Pacific Atlantic Water Flow"