In this article, we will explore the problem of counting the number of “nice” subarrays in a given array of integers. A subarray is considered “nice” if it contains exactly k odd numbers. We’ll delve into understanding the problem, discuss a brute force approach, and then move on to more efficient solutions.

If you’re just joining us, it might be helpful to catch up on the previous entries. Want to see more problem-solving techniques? Follow me here on my blog!


Understanding the Problem
The task is to find the number of subarrays within an array nums that contain exactly k odd numbers. Let’s understand this with some examples:
Example 1:
Input: nums = [1,1,2,1,1], k = 3
Output: 2
Explanation: The only sub-arrays with 3 odd numbers are [1,1,2,1] and [1,2,1,1].
Example 2:
Input: nums = [2,4,6], k = 1
Output: 0
Explanation: There are no odd numbers in the array.
Example 3:
Input: nums = [2,2,2,1,2,2,1,2,2,2], k = 2
Output: 16
Brute Force Approach
A brute force approach would involve generating all possible subarrays and then counting the number of odd numbers in each subarray. If the count matches k, we increment our result count.
def numberOfSubarrays(self, nums: List[int], k: int) -> int:
def countOdds(arr):
odds = 0
for i in range(len(arr)):
if arr[i] % 2 != 0:
odds += 1
return odds
n = len(nums)
all_subarrs = []
for i in range(n):
for j in range(i, n):
all_subarrs.append(nums[i:j+1])
subarrays = 0
for sub_arr in all_subarrs:
if countOdds(sub_arr) == k:
subarrays += 1
return subarrays
Explanation
- countOdds Function: This helper function counts the number of odd numbers in a given array.
- Generating Subarrays: We generate all possible subarrays of the input array.
- Counting Nice Subarrays: For each subarray, we count the odd numbers. If the count matches
k, we increment our result.
Time Complexity: O(n ^ 3) due to the nested loops and counting odds in each subarray.
Space Complexity: O(n ^ 2) for storing all subarrays.
Using Efficient Approach (Prefix Sum and HashMap)
The brute force approach is inefficient, especially for large arrays. A more efficient approach uses a prefix sum and a hashmap to keep track of the count of odd numbers up to the current index. This allows us to determine the number of subarrays ending at the current index with exactly k odd numbers.
By maintaining a running sum of the count of odd numbers and using a hashmap to store these counts, we can quickly find how many subarrays end at the current index and have exactly k odd numbers.
def numberOfSubarrays(self, nums: List[int], k: int) -> int:
curr_sum = 0
subarrays = 0
prefix_sum = { curr_sum: 1 }
for i in range(len(nums)):
curr_sum += nums[i] % 2
if curr_sum - k in prefix_sum:
subarrays = subarrays + prefix_sum[curr_sum - k]
prefix_sum[curr_sum] = prefix_sum.get(curr_sum, 0) + 1
return subarrays
Explanation
- Initialization: We initialize
curr_sumto track the number of odd numbers up to the current index, andprefix_sumto store the frequency of eachcurr_sum. - Updating Prefix Sum: As we iterate through the array, we update
curr_sumbased on whether the current number is odd. - Finding Subarrays: For each index, we check if
curr_sum - kis inprefix_sum. If it is, it means there are subarrays ending at the current index with exactlykodd numbers. - Updating HashMap: We update the hashmap with the current
curr_sum.
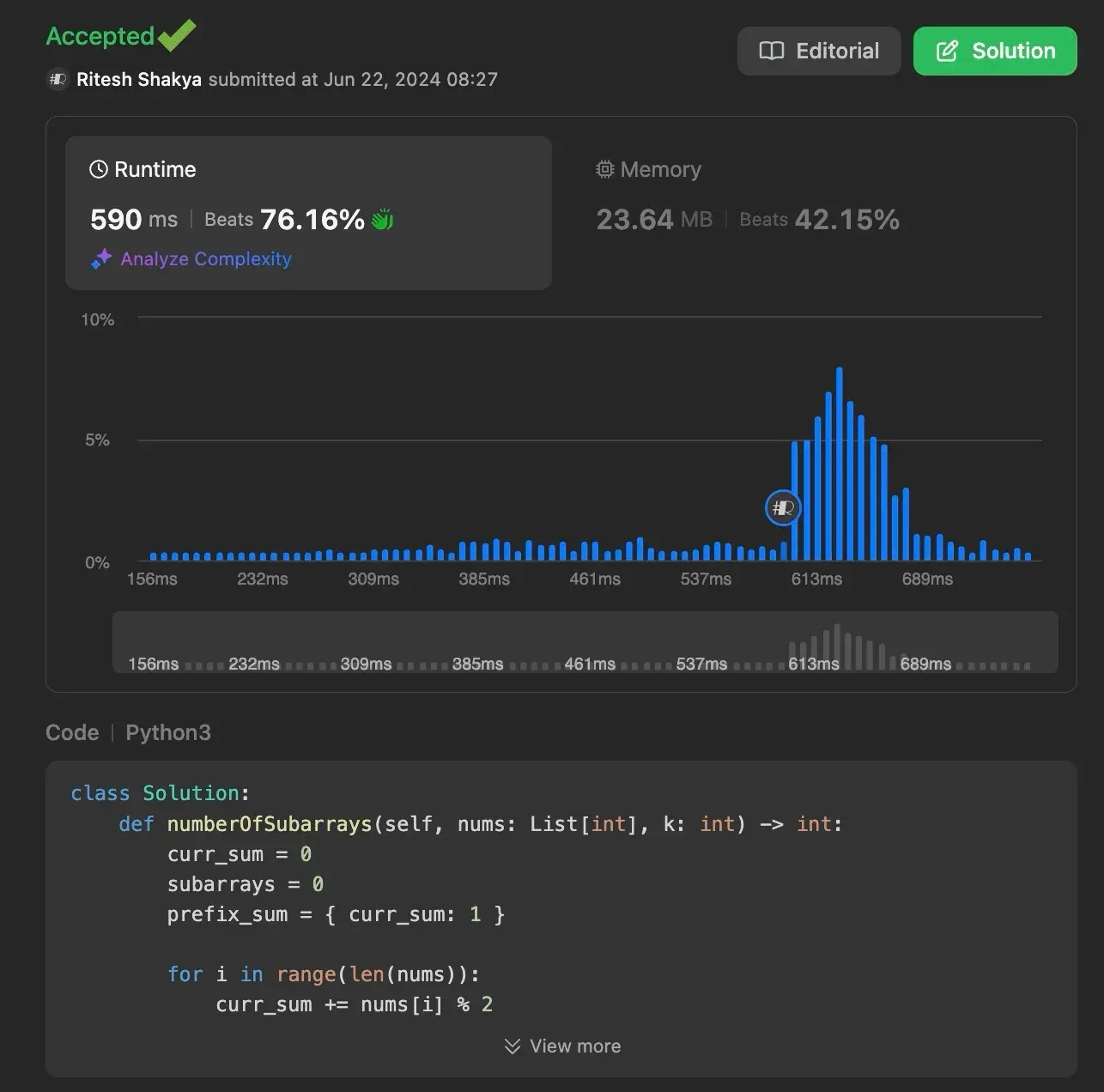
Time Complexity: O(n), where n is the length of the input array.
Space Complexity: O(n) due to the hashmap storing prefix sums.
Using Efficient Approach 2 (Sliding Window)
Another efficient approach is to use the sliding window technique. This method involves maintaining a window that expands until it contains exactly k odd numbers, then it adjusts the starting point of the window to explore all possible subarrays within this window.
The sliding window method allows us to dynamically adjust the start and end of our window, efficiently finding all subarrays with exactly k odd numbers.
def numberOfSubarrays(self, nums: List[int], k: int) -> int:
subarrays = 0
start = 0
qsize = 0
initial_gap = 0
for end in range(len(nums)):
if nums[end] % 2:
qsize += 1
initial_gap = 0
while qsize == k:
initial_gap += 1
if nums[start] % 2:
qsize -= 1
start += 1
subarrays += initial_gap
return subarrays
Explanation
- Initialization: We initialize
subarraysto count the number of nice subarrays,startfor the window’s start,qsizefor the count of odd numbers in the current window, andinitial_gapto count subarrays within the window. - Expanding Window: We expand the window by moving the
endand incrementqsizeif the current number is odd. - Adjusting Start: When the window contains exactly
kodd numbers, we adjust the start of the window and count the possible subarrays. - Counting Subarrays: We add the
initial_gapto the result, representing the number of subarrays within the current window.
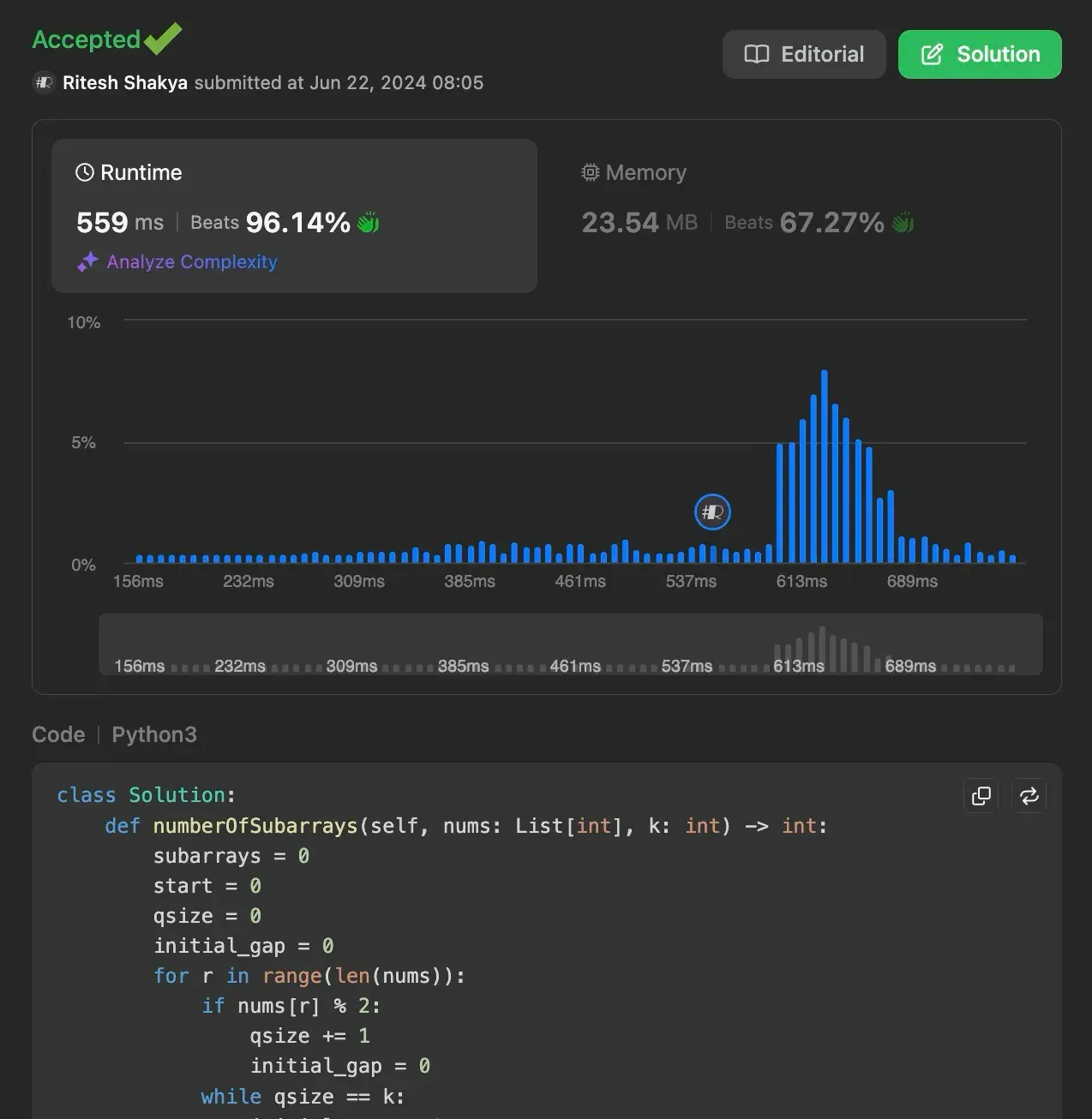
Time Complexity: O(n), where n is the length of the input array.
Space Complexity: O(1) as we use a constant amount of extra space.
Conclusion
In this article, we explored multiple approaches to solve the problem of counting nice subarrays. Starting from a brute force method, we moved to more efficient solutions using prefix sums with hashmaps and the sliding window technique. Efficient problem-solving requires a deep understanding of the problem and the ability to apply the right techniques to optimize performance.
Understanding these methods enhances your problem-solving skills and prepares you for tackling similar challenges in coding interviews and competitions.
Found this helpful? Follow me for more leetcode adventures! Questions? React out via email.
