In this article, we will explore the problem of maximizing the minimum magnetic force between two balls placed in baskets. We’ll look at the problem statement, consider an efficient approach to solve it, and discuss the time and space complexity of our solutions.

If you’re just joining us, it might be helpful to catch up on the previous entries. Want to see more problem-solving techniques? Follow me here on my blog!


Understanding the Problem
The problem is set in a fictional universe where Rick has discovered a special magnetic force between balls placed in baskets. Given n baskets at various positions and m balls, the goal is to distribute the balls into the baskets such that the minimum magnetic force between any two balls is maximized.
The magnetic force between two balls at positions x and y is defined as |x - y|.
Example 1:
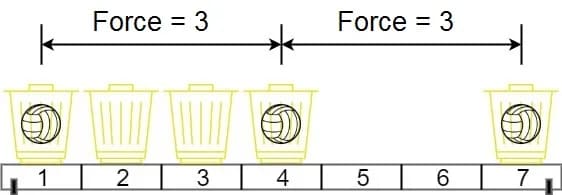
Input: position = [1,2,3,4,7], m = 3
Output: 3
Explanation: Distributing the 3 balls into baskets 1, 4 and 7 will make the magnetic force between ball pairs [3, 3, 6]. The minimum magnetic force is 3. We cannot achieve a larger minimum magnetic force than 3.
Example 2:
Input: position = [5,4,3,2,1,1000000000], m = 2
Output: 999999999
Explanation: We can use baskets 1 and 1000000000.
Using Efficient Approach (Binary Search with Greedy Check)
We will use a binary search to determine the largest minimum distance between the balls. The idea is to check if it’s possible to place all m balls such that the minimum distance between any two balls is at least d. We’ll adjust our search range based on whether it’s possible to place the balls with the current distance d.
def maxDistance(self, position: List[int], m: int) -> int:
position.sort()
if m == 2:
return position[-1] - position[0]
l, r = 1, (position[-1] - position[0])
def canPlaceBalls(distance):
count, last_position = 1, position[0]
for pos in position[1:]:
if pos - last_position >= distance:
count += 1
last_position = pos
if count == m:
return True
return False
while l < r:
mid = (l + r + 1) // 2
if canPlaceBalls(mid):
l = mid
else:
r = mid - 1
return l
Explanation
- Sorting: First, we sort the
positionarray to facilitate easier calculation of distances. - Special Case for
m == 2: If we only have 2 balls, the largest minimum distance is simply the difference between the maximum and minimum positions. - Binary Search Setup: We initialize our search range with
las1andras the maximum possible distance. - Greedy Function (canPlaceBalls): This function checks if it’s possible to place all
mballs with at leastdistancebetween any two balls. - Binary Search Execution: We perform the binary search, adjusting
landrbased on whether thecanPlaceBallsfunction returnsTrueorFalse.
Time Complexity: O(n x log(max_distance)), where n is the number of baskets and max_distance is the difference between the maximum and minimum positions.
Space Complexity: O(1), as we are not using any extra space that scales with input size.
Using Efficient Approach 2 (Binary Search with Tighter Bound)
To further improve the solution, we can optimize the right boundary of our search range. By dividing the maximum possible distance by (m - 1), we can potentially reduce the number of iterations in the binary search. This modification can lead to faster convergence of the binary search.
Why It Works
By tightening the upper bound of our search range, we reduce the number of potential distances to check, which can speed up the binary search process. This approach works because it leverages the fact that the maximum possible minimum distance cannot exceed the evenly distributed distance between the farthest apart baskets divided by the number of balls minus one.
def maxDistance(self, position: List[int], m: int) -> int:
position.sort()
if m == 2:
return position[-1] - position[0]
l, r = 1, (position[-1] - position[0]) // (m - 1)
def canPlaceBalls(distance):
count, last_position = 1, position[0]
for pos in position[1:]:
if pos - last_position >= distance:
count += 1
last_position = pos
if count == m:
return True
return False
while l < r:
mid = (l + r + 1) // 2
if canPlaceBalls(mid):
l = mid
else:
r = mid - 1
return l
Explanation
The code is similar to the first approach, with a slight modification in setting the right boundary (r) of our search range:
- Sorting and Special Case for
m == 2: Similar to the first approach. - Binary Search Setup: We initialize our search range with
las1andras the maximum possible distance divided by(m - 1). - Greedy Function (canPlaceBalls): Same as the first approach.
- Binary Search Execution: Similar to the first approach.
Time Complexity: O(n x log(max_distance)), with a potentially reduced number of iterations due to a tighter bound.
Space Complexity: O(1), as no extra space is used.
Conclusion
In this article, we explored the problem of maximizing the minimum magnetic force between balls placed in baskets. We discussed a brute force approach, an efficient binary search approach combined with a greedy algorithm, and further optimized the solution.
Understanding these methods enhances your problem-solving skills and prepares you for tackling similar challenges in coding interviews and competitions.
Found this helpful? Follow me for more leetcode adventures! Questions? React out via email.
