A LeetCode Daily Series — Day 79

Welcome to today’s blog post where we delve into the problem of maximizing profit by assigning work to workers based on their abilities. We’ll explore the problem, understand various approaches, and implement them in Python. This article is designed to help beginners grasp the concepts and solutions effectively.

Sum Of Square Numbers - LeetCode leetcode.com

Can you solve this real interview question? Sum Of Square Numbers

If you’re just joining us, it might be helpful to catch up on the previous entries. Want to see more problem-solving techniques? Follow me here on my blog!

A LeetCode Daily Series — Introduction | Ritesh Shakya riteshakya.com.np

Hey everyone, I’m excited to announce that I’m embarking on a journey to conquer LeetCode!

Understanding the Problem

You have n jobs and m workers. Each job has a certain difficulty and profit associated with it, given by the arrays difficulty and profit. Each worker has a specific ability, given by the array worker, which indicates the maximum difficulty of the job they can complete. Every worker can be assigned at most one job, but a job can be completed by multiple workers.

Our goal is to assign the jobs to the workers such that the total profit is maximized.

Example 1:

Input: difficulty = [2,4,6,8,10], profit = [10,20,30,40,50], worker = [4,5,6,7]
Output: 100
Explanation: Workers are assigned jobs of difficulty [4,4,6,6] and they get a profit of [20,20,30,30] separately.

Example 2:

Input: difficulty = [85,47,57], profit = [24,66,99], worker = [40,25,25]
Output: 0

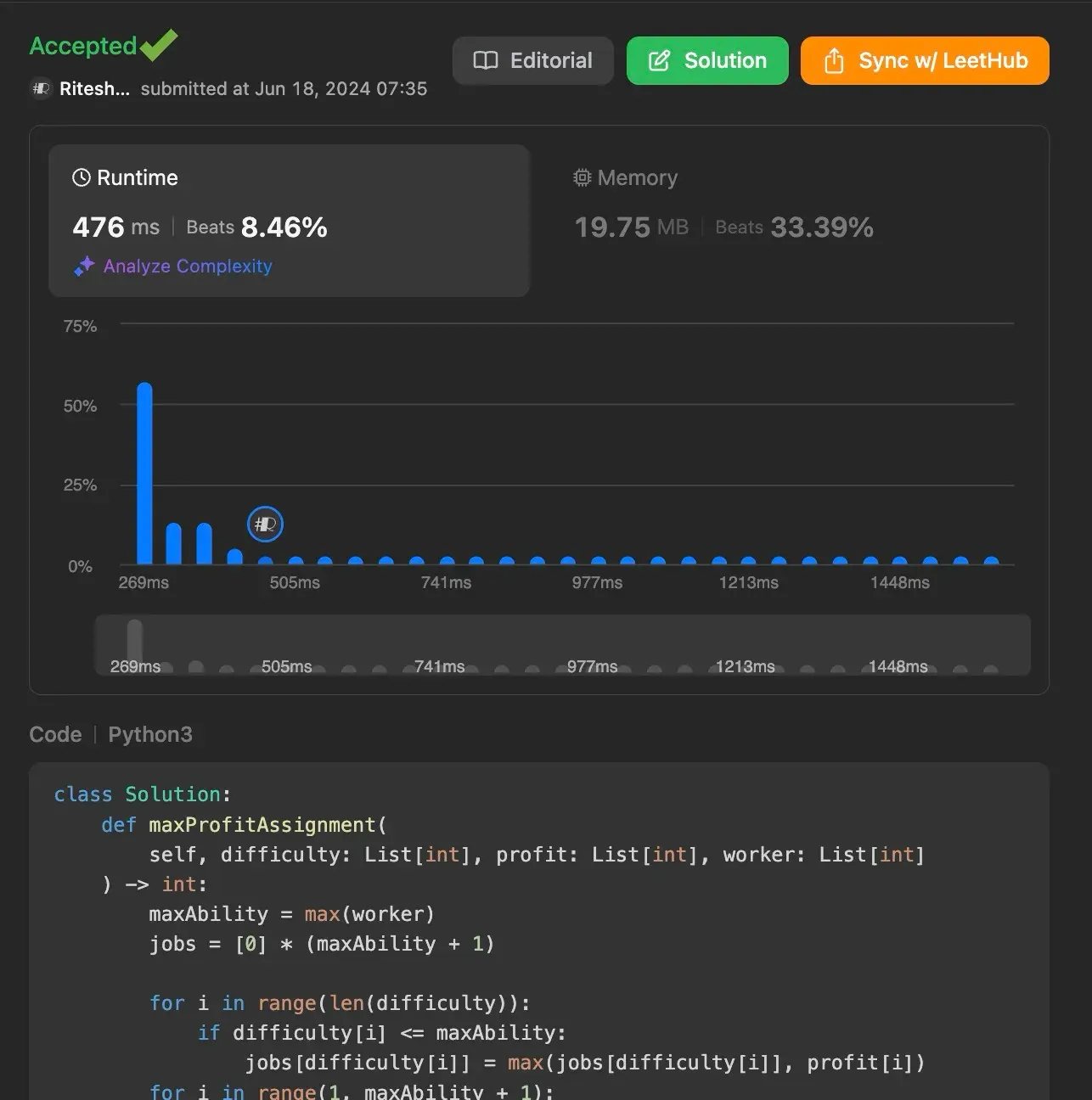
Using Efficient Approach: Dynamic Programming

Dynamic Programming (DP) is a powerful technique that solves problems by breaking them down into simpler subproblems and solving each of these subproblems just once, storing their solutions. Here, we’ll use DP to precompute the best possible profit for every possible worker ability.

def maxProfitAssignment(self, difficulty: List[int], profit: List[int], worker: List[int]) -> int:
    maxAbility = max(worker)
    jobs = [0] * (maxAbility + 1)

    for i in range(len(difficulty)):
        if difficulty[i] <= maxAbility:
            jobs[difficulty[i]] = max(jobs[difficulty[i]], profit[i])

    for i in range(1, maxAbility + 1):
        jobs[i] = max(jobs[i], jobs[i - 1])

    netProfit = 0
    for ability in worker:
        netProfit += jobs[ability]

    return netProfit

Explanation

1. Initialization: We find the maximum ability of the workers and initialize an array jobs to store the maximum profit for each difficulty level up to this ability.
2. Populate Jobs Array: We iterate over the given jobs, updating the jobs array to reflect the maximum profit achievable for each difficulty level.
3. Cumulative Maximum Profit: We update the jobs array such that each entry at index i holds the maximum profit for any job difficulty up to i.
4. Calculate Net Profit: For each worker, we sum up the maximum profit they can achieve based on their ability using the jobs array.

Time Complexity: O(n + m + d), where n is the number of jobs, m is the number of workers, and d is the maximum ability of any worker.

Space Complexity: O(d) due to the jobs array.

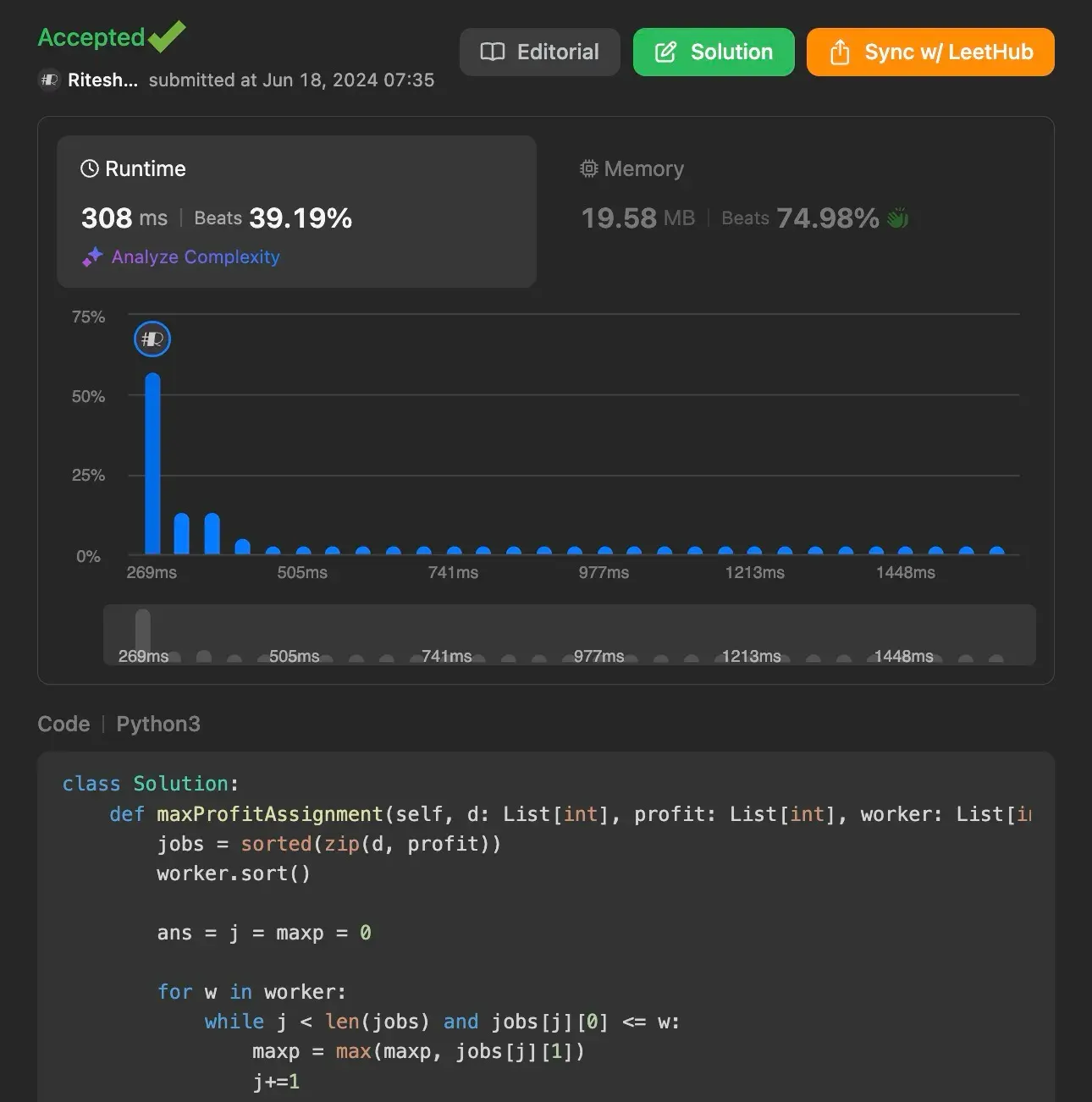
Using Efficient Approach 2: Two Pointers and Sorting

The two-pointer technique combined with sorting is another efficient approach. By sorting both the jobs and workers, we can efficiently assign the best possible job to each worker using a linear scan with two pointers.

def maxProfitAssignment(self, d: List[int], profit: List[int], worker: List[int]) -> int:
    jobs = sorted(zip(d, profit))
    worker.sort()

    ans = j = maxp = 0

    for w in worker:
        while j < len(jobs) and jobs[j][0] <= w:
            maxp = max(maxp, jobs[j][1])
            j += 1
        ans += maxp
    return ans

Explanation

1. Sort Jobs and Workers: We start by sorting the jobs based on their difficulty and the workers based on their ability.
2. Initialize Pointers and Variables: We use j to traverse the jobs and maxp to keep track of the maximum profit we can achieve for the current job.
3. Assign Jobs to Workers: For each worker, we move the job pointer j to find the highest paying job they can complete, updating maxp accordingly.
4. Accumulate Profit: We add the maximum profit that each worker can achieve to the total profit.

Time Complexity: O(n x logn + m x logm), dominated by the sorting operations.

Space Complexity: O(n + m) due to the storage of sorted jobs and workers.

Conclusion

We explored the problem of maximizing profit by assigning work to workers based on their abilities. We discussed two efficient approaches: Dynamic Programming and Two Pointers with Sorting.

Understanding these methods enhances your problem-solving skills and prepares you for tackling similar challenges in coding interviews and competitions.

Found this helpful? Follow me for more leetcode adventures! Questions? React out via email.

Next Articles in the Series

A LeetCode Daily Series — Day 80 | Ritesh Shakya riteshakya.com.np

Today’s problem is called "Minimum Number of Days to Make m Bouquets"