Welcome to another deep dive into algorithmic problem-solving! Today, we are tackling the problem of sorting a linked list in ascending order. We will explore multiple approaches to solve this problem efficiently, including a brute force method, and two optimized solutions using different techniques.

If you’re just joining us, it might be helpful to catch up on the previous entries. Want to see more problem-solving techniques? Follow me here on my blog!


Understanding the Problem#
Given the head of a linked list, the task is to return the list sorted in ascending order. Here are some examples to illustrate the problem:
Example 1:
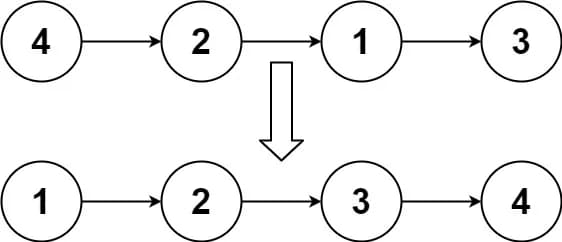
Input: head = [4,2,1,3]
Output: [1,2,3,4]
Example 2:
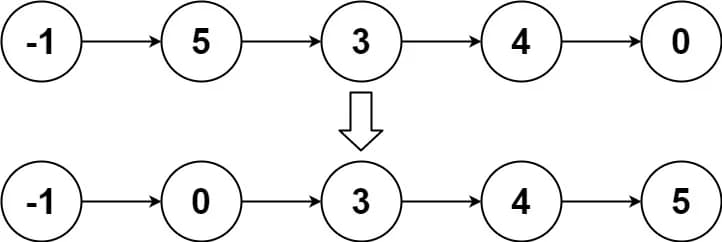
Input: head = [-1,5,3,4,0]
Output: [-1,0,3,4,5]
Example 3:
Input: head = []
Output: []
Brute Force Approach#
The brute force approach involves extracting the values from the linked list into a Python list, sorting the list using a built-in sort method, and then reconstructing the sorted linked list.
def sortList(self, head: Optional[ListNode]) -> Optional[ListNode]:
dummy = ListNode(0)
dummy.next = head
curr = dummy.next
lst = []
while curr:
lst.append(curr.val)
curr = curr.next
lst.sort()
curr = dummy.next
for v in lst:
curr.val = v
curr = curr.next
return dummy.next
Explanation#
- We create a dummy node to facilitate operations on the linked list.
- We traverse the linked list and append all node values to a Python list.
- We sort the list using the sort() method.
- We traverse the linked list again, updating each node’s value with the sorted values from the list.
Time Complexity: O(n x logn) due to the sorting operation.
Space Complexity: O(n) for storing the values in a list.
Using Efficient Approach (Merge Sort)#
Merge Sort is a divide-and-conquer algorithm that works well with linked lists due to their sequential nature. We split the list into halves, sort each half recursively, and then merge the sorted halves.
def sortList(self, head: Optional[ListNode]) -> Optional[ListNode]:
if not head or not head.next:
return head
left = head
right = self.getMid(head)
temp = right.next
right.next = None
right = temp
left = self.sortList(left)
right = self.sortList(right)
return self.merge(left, right)
def getMid(self, head: ListNode):
slow, fast = head, head.next
while fast and fast.next:
slow = slow.next
fast = fast.next.next
return slow
def merge(self, left: ListNode, right: ListNode):
tail = dummy = ListNode()
while left and right:
if left.val < right.val:
tail.next = left
left = left.next
else:
tail.next = right
right = right.next
tail = tail.next
if left:
tail.next = left
if right:
tail.next = right
return dummy.next
Explanation#
- Base Case: If the list is empty or has only one node, it is already sorted, so we return it as is.
- Splitting: Use the
getMidfunction to find the middle of the list. This function uses a slow and fast pointer technique to find the midpoint. - Dividing: Split the list into two halves at the midpoint. The left half starts from the head, and the right half starts from the node after the midpoint.
- Recursion: Recursively sort each half by calling
sortListon both halves. - Merging: Merge the two sorted halves using the merge function
merge. This function compares the nodes of the two halves and merges them into a single sorted list.
Time Complexity: O(n x logn) for splitting and merging.
Space Complexity: O(logn) due to the recursion stack.
Using Efficient Approach 2 (Bottom-Up Merge Sort)#
Bottom-Up Merge Sort iteratively sorts the list by progressively larger sublists, starting with sublists of size one. This avoids recursion and can be more space-efficient.
def sortList(self, head: Optional[ListNode]) -> Optional[ListNode]:
if not head or not head.next:
return head
# get size
size = 0
cur = head
while cur is not None:
cur = cur.next
size += 1
# split
step = 1
dummy = ListNode(None, head)
while step < size:
cur, pre = dummy.next, dummy
while cur is not None:
# split left half
l = r = cur
i = 1
while i < step and r is not None:
r = r.next
i += 1
if r is not None:
tmp = r.next
r.next = None
r = tmp
# split right half
cur = r
i = 1
while i < step and cur is not None:
cur = cur.next
i += 1
if cur is not None:
tmp = cur.next
cur.next = None
cur = tmp
# merge
while l is not None and r is not None:
if l.val <= r.val:
pre.next, l = l, l.next
else:
pre.next, r = r, r.next
pre = pre.next
pre.next = l if l is not None else r
while (nxt := pre.next) is not None: pre = nxt
step <<= 1
return dummy.next
Explanation#
- Calculate Size: First, we determine the size of the linked list by traversing it from the head to the end.
- Iterative Splitting: We use a bottom-up approach to iteratively split the list into sublists of increasing sizes, starting with size one.
- For each step size, we split the list into pairs of sublists of the current step size.
- We maintain pointers for the current sublist (
cur), the previous node (pre), and the left and right halves (landr) of each pair. - We split the list into two halves and move
curandrpointers accordingly.
- Merging Sublists: After splitting, we merge the two sorted halves back together.
- We compare the nodes from the left and right halves (
landr) and link the smaller node to the merged list. - We continue merging until one of the sublists is exhausted, and then link the remaining nodes from the non-exhausted sublist.
- We compare the nodes from the left and right halves (
Time Complexity: O(n x logn) due to iterative splitting and merging.
Space Complexity: O(1) as it avoids recursion and uses a constant amount of extra space, excluding the input and output list space.
Conclusion#
Sorting a linked list efficiently can be achieved through various methods, each with its trade-offs. The brute force approach is simple but not the most efficient. Merge Sort and Bottom-Up Merge Sort provide more optimal solutions, leveraging the structure of the linked list for better performance.
Understanding these methods enhances your problem-solving skills and prepares you for tackling similar challenges in coding interviews and competitions.
Found this helpful? Follow me for more leetcode adventures! Questions? React out via email.
