A LeetCode Daily Series — Day 74

In this article, we will explore the problem of detecting the start of a cycle in a linked list, a common problem in technical interviews and coding challenges. We will delve into the problem, understand the constraints, and walk through both brute force and efficient solutions using detailed code explanations.

Best Time To Buy And Sell Stock With Cooldown - LeetCode leetcode.com

Can you solve this real interview question? Best Time To Buy And Sell Stock With Cooldown

If you’re just joining us, it might be helpful to catch up on the previous entries. Want to see more problem-solving techniques? Follow me here on my blog!

A LeetCode Daily Series — Introduction | Ritesh Shakya riteshakya.com.np

Hey everyone, I’m excited to announce that I’m embarking on a journey to conquer LeetCode!

Understanding the Problem

The problem requires us to determine the starting node of a cycle in a linked list, if such a cycle exists. A cycle occurs if a node in the list can be revisited by continuously following the next pointer. We need to return the node where this cycle begins. If no cycle is present, we return None.

Example 1:

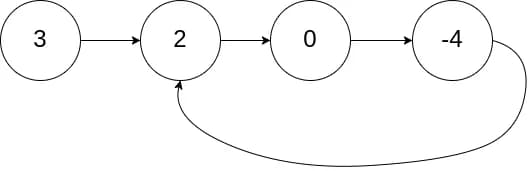
Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.

Example 2:

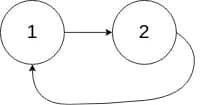
Input: head = [1,2], pos = 0
Output: tail connects to node index 0
Explanation: There is a cycle in the linked list, where tail connects to the first node.

Example 3:

Input: head = [1], pos = -1
Output: no cycle
Explanation: There is no cycle in the linked list.

Brute Force Approach

The brute force approach involves using a hash set to keep track of visited nodes. As we traverse the linked list, we check if a node has already been visited. If a node is encountered again, it indicates the start of the cycle. If we reach the end of the list without revisiting any node, there is no cycle.

def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:
    visited_nodes = set()
    current_node = head

    while current_node:
        if current_node in visited_nodes:
            return current_node
        visited_nodes.add(current_node)
        current_node = current_node.next

    return None

Explanation

1. Initialization: We initialize an empty set visited_nodes to keep track of visited nodes.
2. Traverse the List: We traverse the linked list using a current_node pointer.
3. Cycle Detection: If the current_node is already in the visited_nodes set, it indicates the start of the cycle.
4. Add to Set: If the current_node is not in the set, we add it to the set and move to the next node.
5. Return Result: If no cycle is detected and we reach the end of the list, we return None.

Time Complexity: O(n), where n is the number of nodes in the linked list. We traverse the list once.

Space Complexity: O(n), as we store each node in the set.

Thinking More Efficiently

To solve this problem more efficiently, we use the Floyd’s Tortoise and Hare algorithm, which utilizes two pointers moving at different speeds to detect a cycle.

Using Efficient Approach (Floyd’s Tortoise and Hare Algorithm)

The Floyd’s Tortoise and Hare algorithm is a two-pointer technique used to detect cycles in a linked list. The slow pointer moves one step at a time, while the fast pointer moves two steps at a time. If there is a cycle, the slow and fast pointers will eventually meet. Once a cycle is detected, we can find the starting node of the cycle by resetting one pointer to the head and moving both pointers one step at a time until they meet again.

def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:
    slow, fast = head, head
    while fast and fast.next:
        slow = slow.next
        fast = fast.next.next

        if slow == fast:
            break
    else:
        return None

    pointer = head
    while pointer != fast:
        pointer = pointer.next
        fast = fast.next

    return pointer

Explanation

1. Initialization: We initialize two pointers, slow and fast, both pointing to the head of the linked list.
2. Cycle Detection: We move slow one step and fast two steps in each iteration. If slow meets fast, a cycle is detected.
3. Cycle Entry Point: If a cycle is detected, we reset a pointer to the head and move both pointer and fast one step at a time. The node where they meet is the start of the cycle.
4. Return Result: If no cycle is detected in the initial phase, we return None.

Time Complexity: O(n), where n is the number of nodes in the linked list. Both pointers traverse the list a limited number of times.

Space Complexity: O(1), as we only use two additional pointers for the detection.

Conclusion

Detecting the start of a cycle in a linked list is a common problem that can be solved using both brute force and efficient approaches. The brute force approach, while straightforward, requires additional space. In contrast, the Floyd’s Tortoise and Hare algorithm offers an optimal solution with linear time complexity and constant space complexity.

Understanding these methods enhances your problem-solving skills and prepares you for tackling similar challenges in coding interviews and competitions.

Found this helpful? Follow me for more leetcode adventures! Questions? React out via email.

Next Articles in the Series

A LeetCode Daily Series — Day 75 | Ritesh Shakya riteshakya.com.np

Today’s problem is called "Add Two Numbers"