A LeetCode Daily Series — Day 72

Today’s problem is called "Partition to K Equal Sum Subsets"

Updated: at 01:45 AM

Welcome to another problem-solving journey in the world of algorithms! In this article, we’ll dive into solving the problem of partitioning an integer array into k non-empty subsets with equal sums. We’ll explore the problem, understand different approaches to solving it, and analyze their time and space complexities.

If you’re just joining us, it might be helpful to catch up on the previous entries. Want to see more problem-solving techniques? Follow me here on my blog!

Cover Image

Understanding the Problem

The problem requires us to determine if it’s possible to divide an integer array nums into k non-empty subsets such that the sum of each subset is equal.

Example 1:

Input: nums = [4,3,2,3,5,2,1], k = 4
Output: true
Explanation: It is possible to divide it into 4 subsets (5), (1, 4), (2,3), (2,3) with equal sums.

Example 2:

Input: nums = [1,2,3,4], k = 3
Output: false

Using Efficient Approach: Depth-First Search with Pruning

The goal is to utilize depth-first search (DFS) combined with backtracking to explore potential partitions. We’ll implement an efficient solution by leveraging sorting and pruning techniques to eliminate infeasible paths early, thus reducing computational complexity.

def canPartitionKSubsets(self, nums: List[int], k: int) -> bool:
    n = len(nums)
    target, rem = divmod(sum(nums), k)
    nums.sort(reverse=True)
    if rem or nums[0] > target:
        return False

    used = [False] * n

    def dfs(index, total, k):

        if k == 0:
            return True

        if total == 0:
            return dfs(0, target, k - 1)

        for i in range(index, n):

            if i > 0 and not used[i - 1] and nums[i] == nums[i - 1]:
                continue

            if used[i] or total - nums[i] < 0:
                continue

            used[i] = True
            if dfs(i + 1, total - nums[i], k):
                return True
            used[i] = False
        return False

    return dfs(0, target, k)

Explanation

  1. Initial Setup:
    • Calculate the expected sum (target) for each subset and check if the total sum is divisible by k.
    • If the largest element exceeds target, partitioning is impossible.
  2. DFS Function:
    • The function dfs is defined to try and form subsets recursively.
    • Base Case: If k is zero, it means we’ve successfully formed k subsets and return true.
    • Subset Formation: If the current subset sum (total) reaches zero, we attempt to form the next subset.
    • Element Inclusion: We iterate over elements starting from the given index and attempt to include each element in the current subset:
      • Skip if the current element is the same as the previous and the previous wasn’t used (to avoid duplicates).
      • Skip if the element is already used or if it exceeds the remaining sum required for the current subset.
      • Mark the element as used and recursively attempt to complete the subset.
      • If unsuccessful, backtrack by unmarking the element.

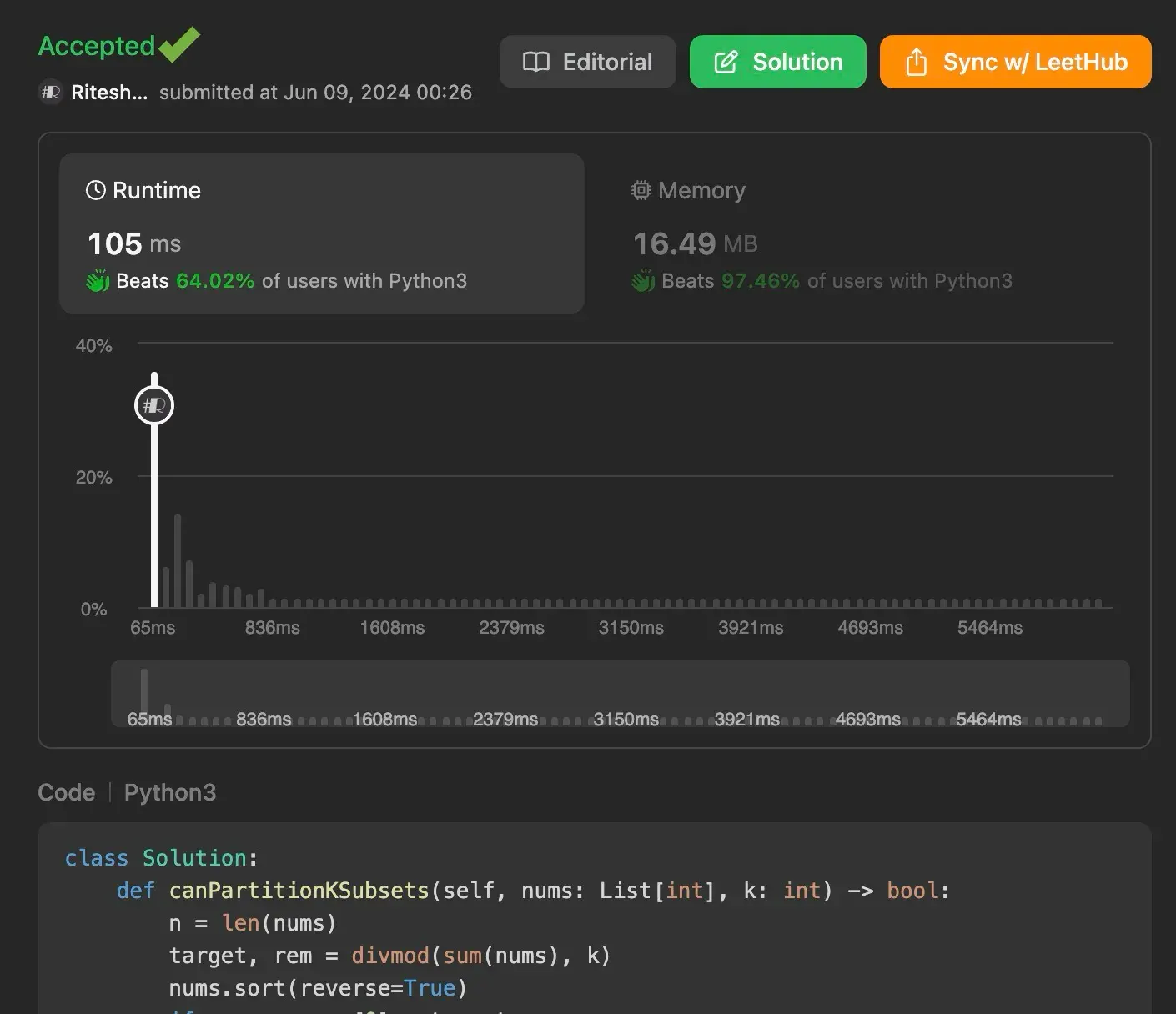
Time Complexity: O(k x 2 ^ n) in the worst case due to the exploration of subsets through recursive calls.

Space Complexity: O(n) for the recursion stack and usage tracking array.

DFS Pruning Result

Using Efficient Approach 2: Optimized DFS with Early Stopping

We further optimize the DFS approach by introducing early stopping conditions and more rigorous pruning strategies. This involves quickly eliminating impossible paths, thereby saving computational effort.

def canPartitionKSubsets(self, nums: List[int], k: int) -> bool:
    n = len(nums)
    target, rem = divmod(sum(nums), k)
    nums.sort(reverse=True)
    if rem or nums[0] > target:
        return False

    def dfs(index, total, groups):
        if groups == k - 1:
            return True
        if index == n:
            return False

        num = nums[index]
        if num > total:
            return dfs(index + 1, total, groups)

        nums[index] = target + 1
        if num == total:
            return dfs(0, target, groups + 1)

        if dfs(index + 1, total - num, groups):
            return True

        nums[index] = num
        return dfs(index + 1, total, groups)

    return dfs(0, target, 0)

Explanation

  1. Initial Checks:
    • Calculate the expected sum (target) for each subset and check if the total sum is divisible by k.
    • If the largest element exceeds target, partitioning is impossible.
  2. DFS Function:
    • Groups Formation: If groups equals k-1, we’ve successfully formed all but one subset and can return True.
    • Early Stopping: If the current index reaches the end, return False.
    • Element Inclusion: Attempt to include the current element in the subset:
      • If it exceeds the target, skip it.
      • Mark the element as used temporarily by setting it to target + 1.
      • If the element exactly matches the target, attempt to form the next group.
      • Recursively try to form subsets by including or excluding the current element.
      • Restore the element value if the current path is not feasible.

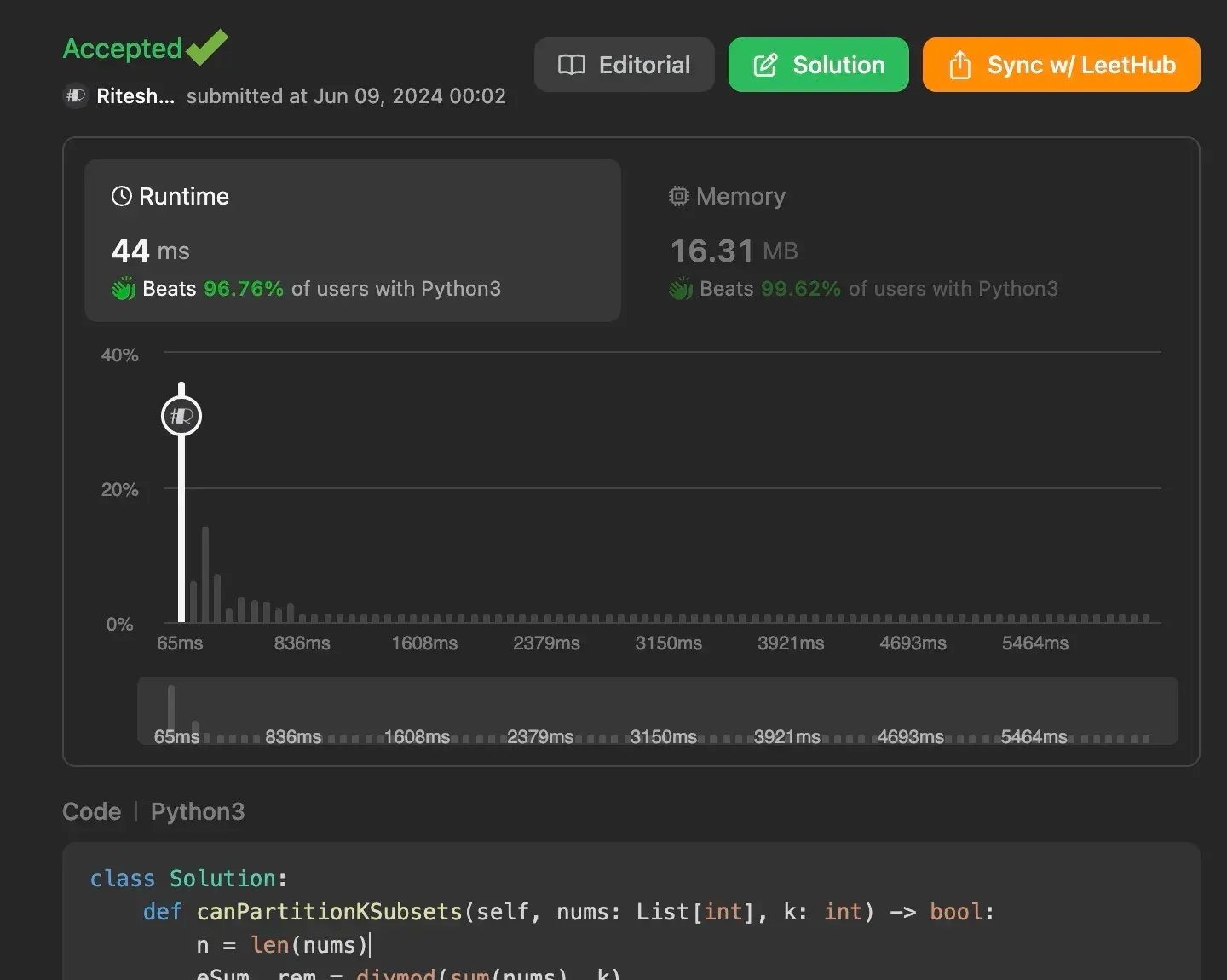
Time Complexity: O(2 ^ n) due to early stopping and optimized DFS.

Space Complexity: O(n) for the recursion stack and in-place array modifications.

Early Stopping Result

Further Details on Optimizations

Initial Sorting

Sorting the array in descending order helps in multiple ways. It allows us to start with the largest numbers, which are more likely to either exceed the target sum or be included in the first few subsets. This early determination can save considerable computational effort by avoiding unnecessary recursive calls.

Early Stopping Conditions

The second approach employs more rigorous early stopping conditions. For instance:

In-Place Modification for Backtracking

Instead of using a separate used array to track included elements, we modify the nums array in place. When an element is considered part of a subset, it’s temporarily marked by setting it to target + 1, which is guaranteed to be greater than any possible subset sum. This marking is undone if the current path doesn’t lead to a solution, maintaining the integrity of the array for other recursive calls.

Conclusion

Partitioning an array into k equal sum subsets is a challenging problem that can be efficiently tackled using DFS with backtracking and pruning. By leveraging these techniques, we can reduce the complexity and solve the problem within feasible time limits for moderate-sized arrays.

Understanding these methods enhances your problem-solving skills and prepares you for tackling similar challenges in coding interviews and competitions.

Found this helpful? Follow me for more leetcode adventures! Questions? React out via email.

Next Articles in the Series