A LeetCode Daily Series — Day 70

In this article, we will explore the problem of finding the number of longest increasing subsequences in a given integer array. This problem presents an interesting challenge, requiring a balance between understanding the concept and implementing an efficient solution. We will discuss the problem in detail, delve into two different approaches to solve it, and provide a challenge for those looking to push their problem-solving skills further.

Palindromic Substrings - LeetCode leetcode.com

Can you solve this real interview question? Palindromic Substrings

If you’re just joining us, it might be helpful to catch up on the previous entries. Want to see more problem-solving techniques? Follow me here on my blog!

A LeetCode Daily Series — Introduction | Ritesh Shakya riteshakya.com.np

Hey everyone, I’m excited to announce that I’m embarking on a journey to conquer LeetCode!

Understanding the Problem

The problem is to determine the number of longest strictly increasing subsequences in a given integer array. Given an array nums, we need to return the number of subsequences that are the longest and strictly increasing.

Example 1:

Input: nums = [1,3,5,4,7]
Output: 2
Explanation: The two longest increasing subsequences are [1, 3, 4, 7] and [1, 3, 5, 7].

Example 2:

Input: nums = [2,2,2,2,2]
Output: 5
Explanation: The length of the longest increasing subsequence is 1, and there are 5 increasing subsequences of length 1, so output 5.

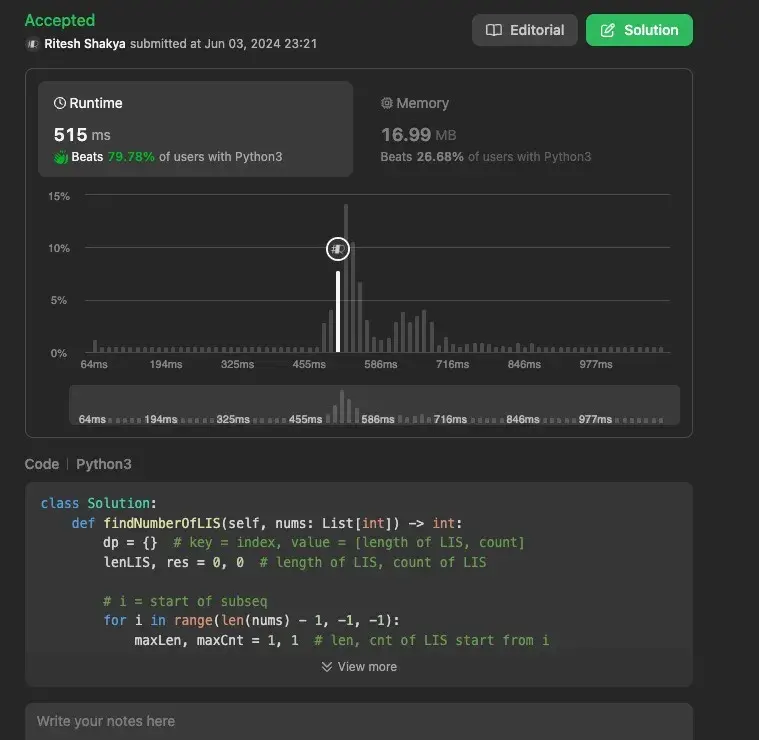
Using Efficient Approach (Dynamic Programming with HashMap)

This approach utilizes dynamic programming combined with a hash map to store the lengths and counts of the longest increasing subsequences starting from each index. This method ensures that we efficiently compute the required values without redundant calculations.

def findNumberOfLIS(self, nums: List[int]) -> int:
    dp = {}
    lenLIS, res = 0, 0

    for i in range(len(nums) - 1, -1, -1):
        maxLen, maxCnt = 1, 1

        for j in range(i + 1, len(nums)):
            if nums[j] > nums[i]:
                length, count = dp[j]
                if length + 1 > maxLen:
                    maxLen, maxCnt = length + 1, count
                elif length + 1 == maxLen:
                    maxCnt += count
        if maxLen > lenLIS:
            lenLIS, res = maxLen, maxCnt
        elif maxLen == lenLIS:
            res += maxCnt
        dp[i] = [maxLen, maxCnt]

    return res

Explanation

1. Initialization:

   • dp is a dictionary where the key is the index and the value is a list containing the length of the longest increasing subsequence starting at that index and its count.
   • lenLIS keeps track of the length of the longest increasing subsequence found.
   • res keeps track of the number of such longest increasing subsequences.

2. Iterating from the end: We iterate from the end of the array to the beginning. For each index i, we initialize maxLen and maxCnt to 1 because the minimum length of LIS starting from i is 1.

3. Inner Loop:

   • We check all subsequent elements to see if they can extend the increasing subsequence starting at i.
   • If nums[j] > nums[i], we update maxLen and maxCnt based on the length and count stored at dp[j].

4. Updating Results:

   • After processing i, if maxLen exceeds lenLIS, we update lenLIS and set res to maxCnt.
   • If maxLen is equal to lenLIS, we increment res by maxCnt.

5. Storing Results: Store the computed maxLen and maxCnt for index i in the dp dictionary.

Time Complexity: O(n^2), where n is the length of the array. This is due to the nested loops iterating through the array.

Space Complexity: O(n), for storing the dp dictionary.

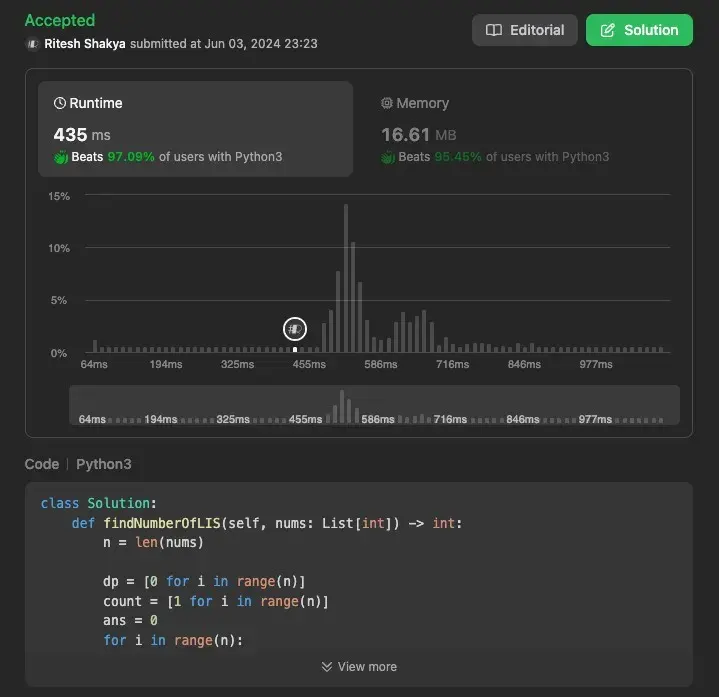
Using Efficient Approach 2 (Dynamic Programming with Arrays)

This approach uses dynamic programming with arrays to store the lengths and counts of the longest increasing subsequences. It leverages two arrays to keep track of the lengths of the LIS ending at each index and the count of such subsequences.

def findNumberOfLIS(self, nums: List[int]) -> int:
    n = len(nums)

    dp = [0 for i in range(n)]
    count = [1 for i in range(n)]
    ans = 0
    for i in range(n):
        temp = 0
        for j in range(i):
            if nums[j] < nums[i]:
                if temp < dp[j]:
                    temp = dp[j]
                    count[i] = count[j]
                elif dp[j] == temp:
                    count[i] += count[j]
        dp[i] = temp + 1
        if dp[i] > dp[ans]:
            ans = i
    sol = 0
    for i in range(n):
        if dp[i] == dp[ans]:
            sol += count[i]
    return sol

Explanation

1. Initialization:

   • dp is an array where dp[i] represents the length of the LIS ending at index i.
   • count is an array where count[i] represents the number of LIS ending at index i.
   • ans is used to keep track of the index of the longest LIS found.

2. Outer Loop: Iterate through each index i to compute the LIS ending at i.

3. Inner Loop:

   • For each i, iterate through all previous indices j to check if nums[j] < nums[i].
   • If nums[j] < nums[i], update the temporary length temp and count count[i] accordingly.

4. Updating dp and ans:

   • Update dp[i] to temp + 1.
   • If the new LIS length at i is greater than the length at ans, update ans.

5. Calculating Result: Iterate through dp to count the number of LIS of maximum length found.

Time Complexity: O(n^2), due to the nested loops iterating through the array.

Space Complexity: O(n), for storing the dp and count arrays.

Conclusion

In this article, we explored the problem of finding the number of longest increasing subsequences in a given integer array. We discussed two efficient approaches using dynamic programming with a hash map and arrays.

Understanding these methods enhances your problem-solving skills and prepares you for tackling similar challenges in coding interviews and competitions.

Found this helpful? Follow me for more leetcode adventures! Questions? React out via email.

Next Articles in the Series

A LeetCode Daily Series — Day 71 | Ritesh Shakya riteshakya.com.np

Today’s problem is called "Partition Equal Subset Sum"