A LeetCode Daily Series — Day 68

Welcome to another exploration of algorithmic problem-solving! Today, we delve into the “Jump Game” problem, a popular challenge that requires strategic thinking and an understanding of dynamic programming and greedy algorithms. This problem is frequently encountered in coding interviews and competitive programming, making it an excellent addition to your problem-solving toolkit.

Jump Game - LeetCode leetcode.com

Can you solve this real interview question? Jump Game

If you’re just joining us, it might be helpful to catch up on the previous entries. Want to see more problem-solving techniques? Follow me here on my blog!

A LeetCode Daily Series — Introduction | Ritesh Shakya riteshakya.com.np

Hey everyone, I’m excited to announce that I’m embarking on a journey to conquer LeetCode!

Understanding the problem

You are given an integer array nums, where each element represents your maximum jump length at that position. Starting from the first index, your goal is to determine whether you can reach the last index of the array.

Here are two examples to illustrate the problem:

Example 1:

Input: nums = [2,3,1,1,4]
Output: true
Explanation: Jump 1 step from index 0 to 1, then 3 steps to the last index.

Example 2:

Input: nums = [3,2,1,0,4]
Output: false
Explanation: You will always arrive at index 3 no matter what. Its maximum jump length is 0, which makes it impossible to reach the last index.

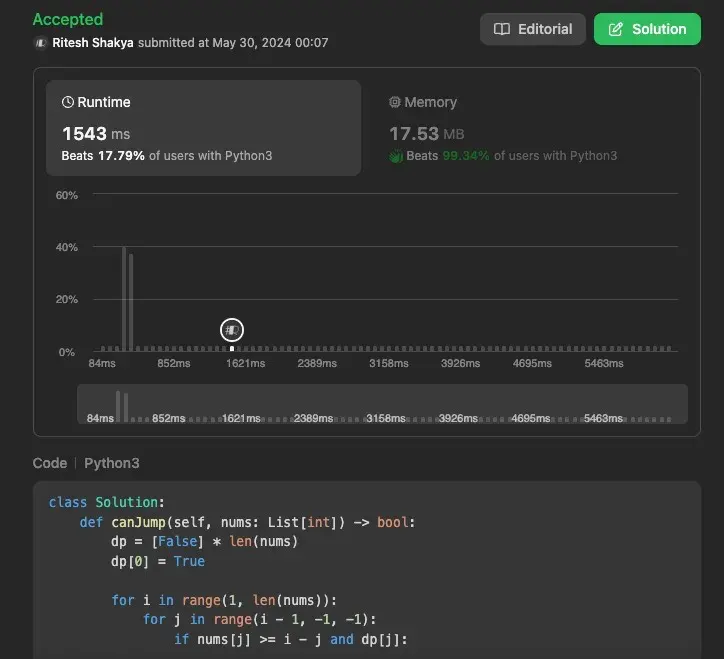
Using Efficient Approach 1: Dynamic Programming

Dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is particularly useful when the problem has overlapping subproblems and optimal substructure properties.

In this approach, we use a boolean array dp where dp[i] indicates whether the position i is reachable. We initialize dp[0] to True because the starting point is always reachable.

def canJump(self, nums: List[int]) -> bool:
    dp = [False] * len(nums)
    dp[0] = True

    for i in range(1, len(nums)):
        for j in range(i - 1, -1, -1):
            if nums[j] >= i - j and dp[j]:
                dp[i] = True
                break

    return dp[-1]

Explanation

1. Initialization: Create a list dp of the same length as nums and initialize all elements to False. Set dp[0] to True since we start from the first index.
2. Nested Loop: The outer loop iterates through each index i from 1 to the end of the array. The inner loop checks all previous indices j to see if the position i can be reached from j.
3. Condition Check: If nums[j] is greater than or equal to the distance from j to i and dp[j] is True, then dp[i] is set to True.
4. Return Result: Finally, return the value of dp[-1], which indicates whether the last index is reachable.

Time Complexity: O(n^2), where n is the length of the array. This is because, in the worst case, for each element, we might check all previous elements.

Space Complexity: O(n), due to the additional space required for the dp array.

Using Efficient Approach 2: Greedy Algorithm

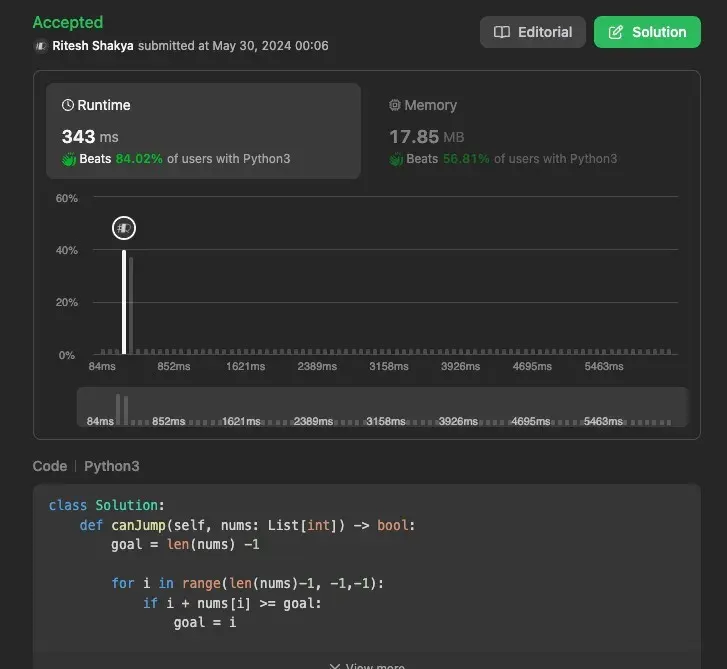
The Greedy Algorithm is another powerful technique that makes the optimal choice at each step with the hope of finding the global optimum. For the Jump Game problem, the greedy approach focuses on updating the farthest reachable index at each step.

def canJump(self, nums: List[int]) -> bool:
    goal = len(nums) -1

    for i in range(len(nums)-1, -1,-1):
        if i + nums[i] >= goal:
            goal = i

    return True if goal == 0 else False

Explanation

1. Initialization: Set goal to the last index of the array.
2. Backward Iteration: Iterate from the last index to the first index.
3. Condition Check: For each index i, check if i + nums[i] is greater than or equal to the goal. If so, update the goal to the current index i.
4. Return Result: After the loop, check if the goal has been updated to 0. If yes, return True; otherwise, return False.

Time Complexity: O(n), where n is the length of the array. This is because we iterate through the array once.

Space Complexity: O(1), since no additional space proportional to the input size is used.

Conclusion

In this article, we explored the Jump Game problem and solved it using two efficient approaches: Dynamic Programming and the Greedy Algorithm. Each approach has its own advantages and trade-offs in terms of time and space complexity.

Understanding these methods enhances your problem-solving skills and prepares you for tackling similar challenges in coding interviews and competitions.

Found this helpful? Follow me for more leetcode adventures! Questions? React out via email.

Next Articles in the Series

A LeetCode Daily Series — Day 69 | Ritesh Shakya riteshakya.com.np

Today’s problem is called "Palindromic Substrings"