Welcome to this deep dive into solving the Unique Paths problem. We’ll explore different strategies to efficiently determine the number of unique paths a robot can take on an m×n grid, starting from the top-left corner and moving to the bottom-right corner.

If you’re just joining us, it might be helpful to catch up on the previous entries. Want to see more problem-solving techniques? Follow me here on my blog!


Understanding the Problem
The problem at hand involves finding the number of unique paths on a grid where the robot can only move either right or down. Given the grid’s dimensions m and n, our task is to compute the number of such paths.
To better illustrate the problem, consider the following examples:
Example 1:
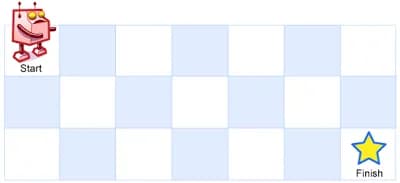
Input: m = 3, n = 7
Output: 28
Example 2:
Input: m = 3, n = 2
Output: 3
Explanation: From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down
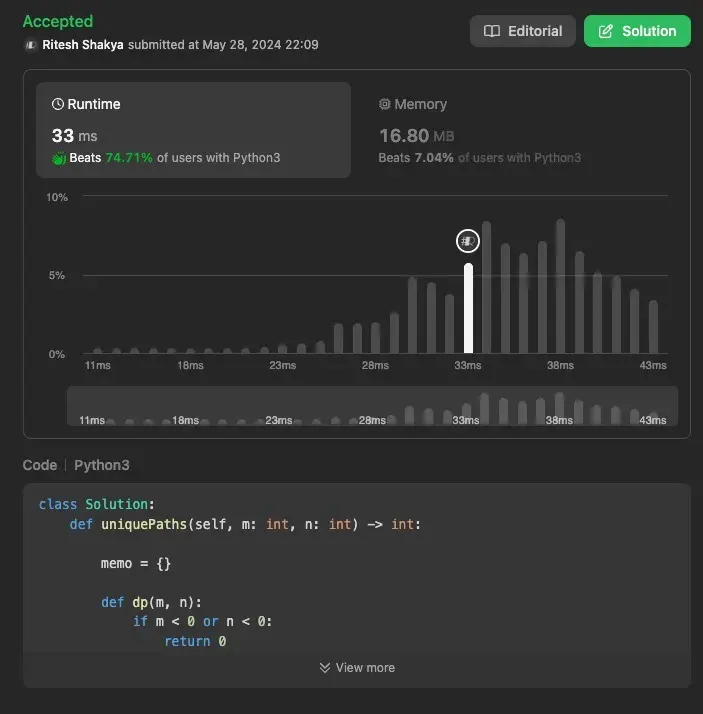
Using Efficient Approach 2 (Memoization)
Memoization is another efficient technique that involves storing the results of expensive function calls and reusing them when the same inputs occur again. This avoids redundant computations and significantly speeds up the process.
def uniquePaths(self, m: int, n: int) -> int:
memo = {}
def dp(m, n):
if m < 0 or n < 0:
return 0
if m == 1 or n == 1:
return 1
if (m, n) in memo:
return memo[(m, n)]
memo[(m, n)] = dp(m - 1, n) + dp(m, n - 1)
return memo[(m, n)]
return dp(m, n)
Explanation
- Initialization: We create a dictionary
memoto store the results of subproblems. - Base Cases: If
mornis less than 0, we return 0 (invalid cell). Ifmornis 1, we return 1 (only one way to reach the edge cells). - Memoization: For each cell
(m, n), we check if its result is already computed. If not, we compute it by summing the results of the cell above (dp(m - 1, n)) and the cell to the left (dp(m, n - 1)), and store it in memo. - Result: Finally, we return the result for the initial cell
(m, n).
Time Complexity: O(m×n). Each subproblem is solved once and stored in the memo.
Space Complexity: O(m×n). We use a dictionary to store the results of all subproblems.
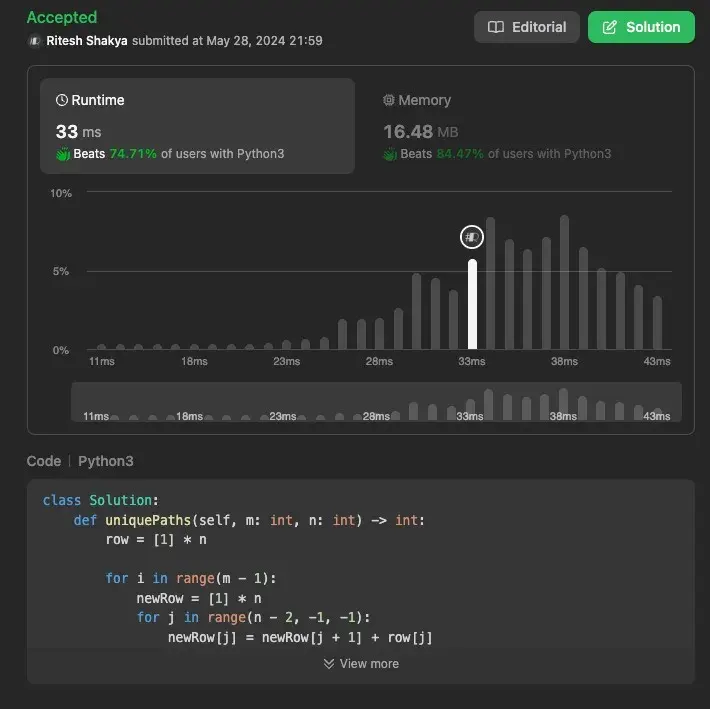
Using Efficient Approach (Dynamic Programming)
Dynamic programming (DP) is a powerful technique used to solve problems by breaking them down into simpler subproblems. For this problem, we can utilize a 1D DP array to store the number of ways to reach each cell in the grid.
def uniquePaths(self, m: int, n: int) -> int:
row = [1] * n
for i in range(m - 1):
newRow = [1] * n
for j in range(n - 2, -1, -1):
newRow[j] = newRow[j + 1] + row[j]
row = newRow
return row[0]
Explanation
- Initialization: We initialize a list
rowwithnelements, all set to1. This represents the number of ways to reach each cell in the first row. - Iteration: We iterate through each row (excluding the last one, as it’s the base case).
- Update Rows: For each cell in the current row, we calculate the number of ways to reach it by adding the number of ways to reach the cell directly to the right (
newRow[j + 1]) and the cell directly above (row[j]). - Result: The value at
row[0]gives us the total number of unique paths from the top-left to the bottom-right corner.
Time Complexity: O(m×n). We iterate over each cell in the grid once.
Space Complexity: O(n). We use a 1D array of size n to store the number of ways to reach each cell.
Conclusion
In this article, we explored two efficient approaches to solve the Unique Paths problem: Dynamic Programming and Memoization. Both methods significantly reduce the time complexity compared to a brute force approach, making them suitable for large grids.
Understanding these techniques will not only help you solve this problem but also enhance your problem-solving skills for other grid-based challenges.
Found this helpful? Follow me for more leetcode adventures! Questions? React out via email.
