In this article, we will explore a popular coding problem: Decode Ways. This problem is a great exercise in dynamic programming and helps improve our understanding of how to approach problems with multiple valid solutions. We will delve into the problem, discuss two efficient approaches to solve it, and finally, challenge you to push your skills further.

If you’re just joining us, it might be helpful to catch up on the previous entries. Want to see more problem-solving techniques? Follow me here on my blog!


Understanding the Problem#
Given a string containing only digits, we need to determine the number of ways to decode it using the mapping from ‘A’ to ‘Z’ (where ‘A’ = “1”, ‘B’ = “2”, …, ‘Z’ = “26”). Each digit or pair of digits can be translated into a letter. For example, the string “11106” can be decoded into “AAJF” (1 1 10 6) or “KJF” (11 10 6). However, a grouping like “1 11 06” is invalid since “06” cannot be translated into ‘F’.
Example 1:
Input: s = "12"
Output: 2
Explanation: "12" could be decoded as "AB" (1 2) or "L" (12).
Example 2:
Input: s = "226"
Output: 3
Explanation: "226" could be decoded as "BZ" (2 26), "VF" (22 6), or "BBF" (2 2 6).
Example 3:
Input: s = "06"
Output: 0
Explanation: "06" cannot be mapped to "F" because of the leading zero ("6" is different from "06").
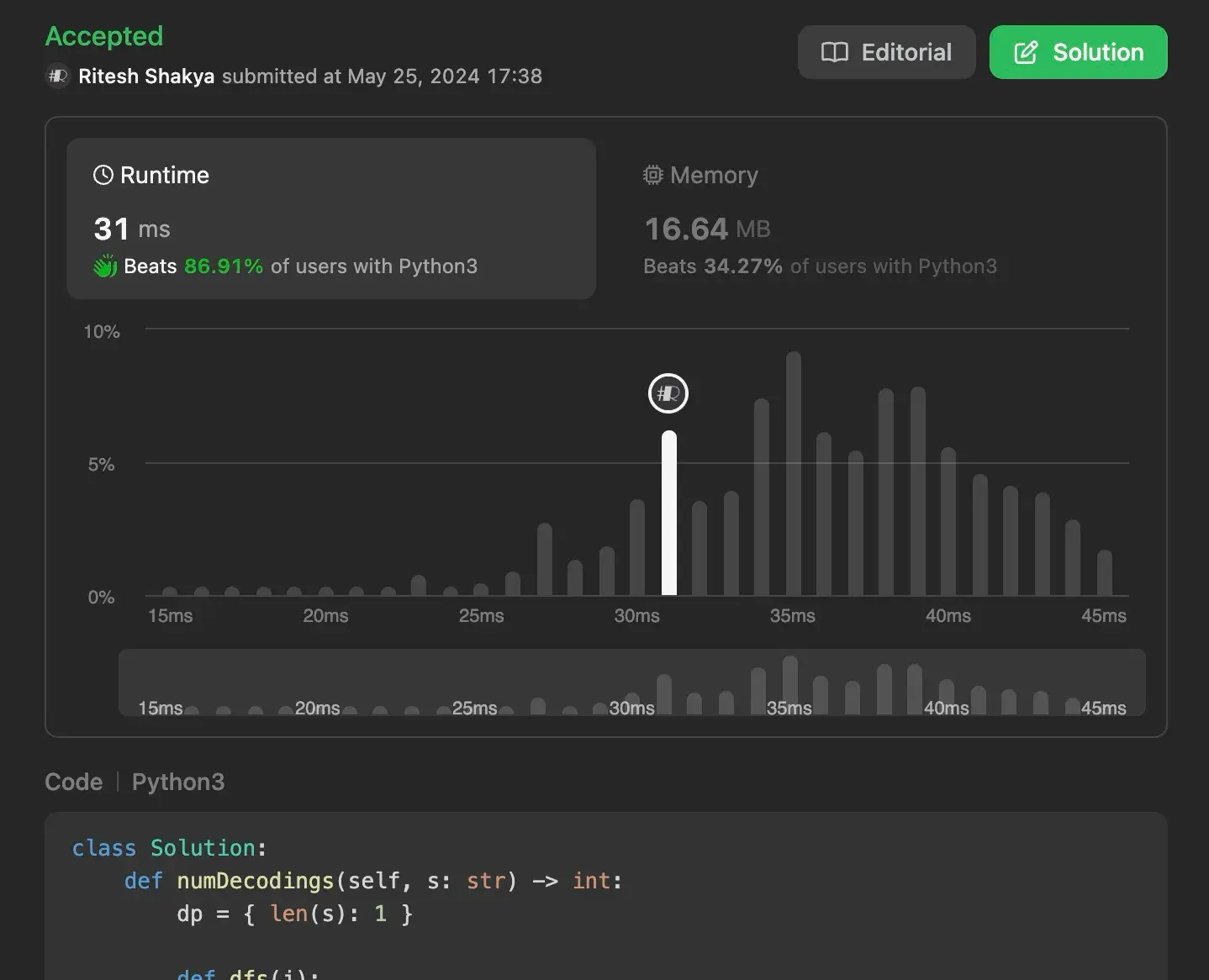
Using Efficient Approach: Depth-First Search (DFS) with Memoization#
This approach uses a depth-first search (DFS) strategy combined with memoization to avoid redundant calculations. The idea is to traverse the string and explore all possible decoding options, storing results of subproblems to reuse them later.
def numDecodings(self, s: str) -> int:
dp = { len(s): 1 }
def dfs(i):
if i in dp:
return dp[i]
if s[i] == "0":
return 0
res = dfs(i + 1)
if i + 1 < len(s) and (
s[i] == "1" or s[i] == "2" and s[i + 1] in "0123456"
):
res += dfs(i + 2)
dp[i] = res
return res
return dfs(0)
Explanation#
- Initialization: A dictionary
dpis initialized withdp[len(s)] = 1, representing the base case where an empty substring has one way to decode (doing nothing). - DFS Function: The
dfsfunction is defined to return the number of ways to decode the substring starting from indexi. - Memoization Check: If
iis already indp, the function returnsdp[i]to avoid redundant calculations. - Handling ‘0’: If
s[i]is ‘0’, it returns0since no valid encoding starts with ‘0’. - Single Digit Decoding: The result
resstarts with the number of ways to decode the substring fromi + 1. - Two Digit Decoding: If the next two characters form a valid encoding (i.e., between 10 and 26), res is incremented by the number of ways to decode the substring from
i + 2. - Memoization Update: The result is stored in
dp[i]and returned.
Time Complexity: O(n), where n is the length of the string. Each index is visited at most once due to memoization.
Space Complexity: O(n), for the recursion stack and memoization dictionary.
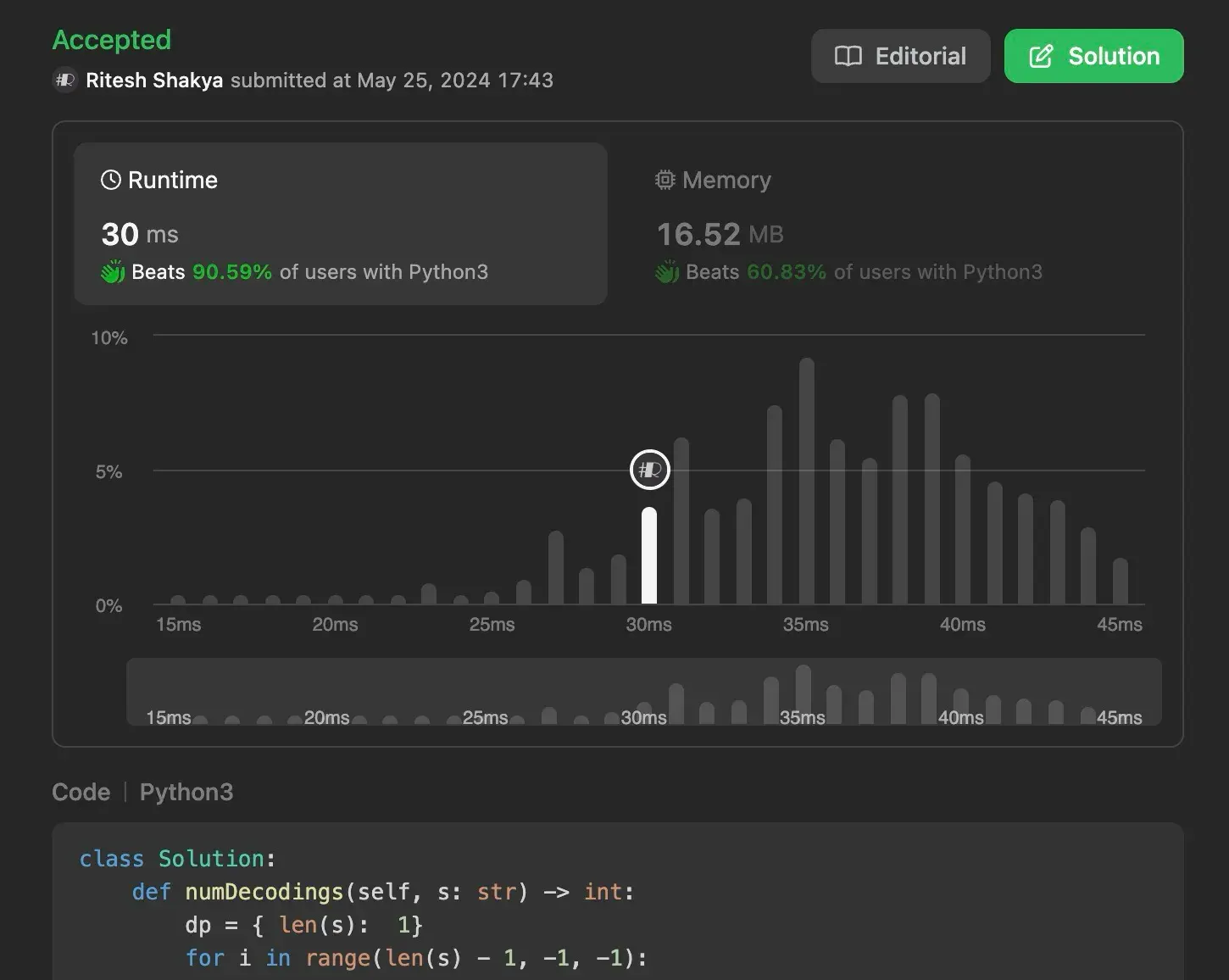
Using Efficient Approach 2: Dynamic Programming (Bottom-Up)#
This approach uses dynamic programming in a bottom-up manner, iterating from the end of the string to the beginning. It builds up the solution iteratively and avoids the overhead of recursive calls.
def numDecodings(self, s: str) -> int:
dp = { len(s): 1 }
for i in range(len(s) - 1, -1, -1):
if s[i] == "0":
dp[i] = 0
else:
dp[i] = dp[i + 1]
if i + 1 < len(s) and (
s[i] == "1" or s[i] == "2" and s[i + 1] in "0123456"
):
dp[i] += dp[i + 2]
return dp[0]
Explanation#
- Initialization: A dictionary
dpis initialized withdp[len(s)] = 1, the base case where an empty substring has one way to decode. - Iteration: A loop runs backwards from the end of the string to the beginning.
- Handling ‘0’: If
s[i]is ‘0’,dp[i]is set to0. - Single Digit Decoding:
dp[i]is set todp[i + 1], representing the ways to decode the substring starting from the next character. - Two Digit Decoding: If the next two characters form a valid encoding,
dp[i]is incremented bydp[i + 2]. - Result: The result is stored in
dp[0], representing the number of ways to decode the entire string.
Time Complexity: O(n), where n is the length of the string. Each index is processed once in the loop.
Space Complexity: O(n), for the dictionary storing the number of ways to decode from each index.
Conclusion#
The Decode Ways problem is a fantastic exercise in dynamic programming, showcasing the importance of efficient problem-solving techniques like memoization and iterative dynamic programming. By breaking down the problem and exploring multiple approaches, we not only find the solution but also enhance our problem-solving toolkit.
Each approach has its trade-offs in terms of time and space complexity, and choosing the right approach depends on the constraints of the problem and the size of the input.
Found this helpful? Follow me for more leetcode adventures! Questions? React out via email.
